Machine Learning: AKTU question paper with answers offers a comprehensive set of exam-oriented questions and detailed solutions, providing B.Tech students with valuable practice material for machine learning examinations
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Machine Learning: *Quantum *B.tech-Syllabus *Circulars *B.tech AKTU RESULT * Btech 4th Year
Section A: Short Question Machine Learning
a. What is purpose of The Inductive Learning Hypothesis ?
Ans. The purpose of inductive learning hypothesis is to predict outputs of given inputs that it has not encountered.
b. Write the TPE for Handwriting Recognition Problem.
Ans. For handwriting recognition learning problem, TPE would be :
Task, T: To recognize and classify handwritten words within the given images.
Performance measure, P: Total percent of words being correctly classified by the program.
Training experience, E: A set of handwritten words with given classifications/Mabels.
c. What is formula of Information Gain in Decision Tree Learning Algorithm ?
Ans.
- i. Information gain is used by ID3 as a criterion for choosing attributes.
- ii. Information gain is the difference between the old requirement for information gain (which was based on the percentage of classes) and the new criteria (i.e. obtained after the partitioning of A).
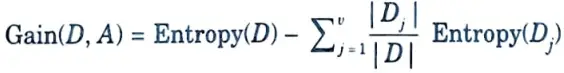
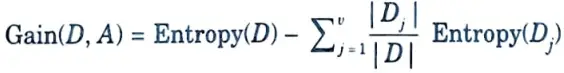
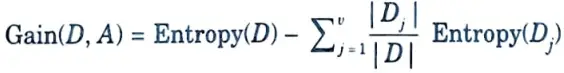
Where,
D : A given data partition
A : Attribute
V : Suppose we partition the tuples in D on some attribute A having V distinct values
- iii. D is split into V partition or subsets, (D1, D2, ..Dj) where Dj contains those tuples in D that have outcome aj, of A.
- iv. The attribute that has the highest information gain is chosen.
d. What is the role of Activation Function in ANN ?
Ans. A neuron’s activation function determines whether or not it will be transported to the next layer and become active. Simply said, it will determine whether or not the neuron’s input to the network is significant to the prediction process.
e. Differentiate between Bias and Variance in ML.
Ans. Bias is the model’s use of simplifications to make the goal function more approachable. Variance is the degree to which different training sets will cause the estimate of the target function to vary.
f. What are Confidence Intervals in ML ?
Ans. The confidence interval is a range in which we may be sure the genuine value is present. The probability that a confidence interval will contain the real parameter value depends on the confidence level that is chosen for the interval. The phrase “Confidence Interval” refers to the range of values that is typically used to handle population-based data, extracting precise, important information with a given level of confidence.
g. What is Lazy Learning ?
Ans. As opposed to eager learning, where the system seeks to generalise the training data before receiving queries, lazy learning theoretically delays generalisation of the training data until a query is made to the system.
h. What is K in KNN Learning?
Ans. K in KNN is a parameter that refers to the number of nearest neighbours to include in the majority of the voting process.
i. What is Value-based reinforcement Learning ?
Ans. A key idea in reinforcement learning RL is value learning. As fundamental as the fully linked network in Deep Learning, it serves as a starting point for learning RL. It calculates how good it is to get to a specific state or do a certain thing.
j. What is the Bellman Equation in Reinforcement Learning ?
Ans.
- 1. A key component of many Reinforcement Learning algorithms is the Bellman equation.
- 2. The value function is divided into two components by the Bellman equation: the current reward and the discounted future values.
- 3. This equation makes it easier to compute the value function, allowing us to identify the best solution to a complicated problem by decomposing it into smaller, recursive subproblems and determining the best answers to those as well.
Section B : Concept Learning Questions in Machine Learning
a. Giving an example, Explain the Concept Learning Task in ML.
Ans.
- 1. The task learning, in contrast to learning from observations, can be described by being given a set of training data {(Ā1, C’1), (Ā2, C’2),….,(Ān, C’n)}, where the Āi – [Ā1i, Āi2,…., Ai1]T with Ai1 ∈ A represent the observable part of the data (here denoted as vector of attributes in the common formalism) and the C’1 represent a valuation of this data.
- 2. If a functional relationship between the Āi and C’1 values is to be discovered, this task is either called regression (in the statistics domain ) or supervised learning (in the machine learning domain).
- 3. The more special case where the C’ values are restricted to some finite set C’ is called classification or concept learning in computational learning theory.
- 4. The classical approach to concept learning is concerned with learning concept descriptions for predefined classes Ci of entities from E.
- 5. A concept is regarded as a function mapping attribute values Āi of discrete attributes to a Boolean value indicating concept membership.
- 6. In this case, the set of entities E is defined by the outer product over the range of the considered attributes in A.
- 7. Concepts are described as hypotheses, i.e., the conjunction of restrictions on allowed attribute values like allowing just one specific, a set of or any value for an attribute.
- 8. The task of classical concept learning consists of finding a hypothesis for each class Ci that matches the training data.
- 9. This task can be performed as a directed search in hypotheses space by exploiting a pre-existing ordering relation, called general to specific ordering of hypotheses.
- 10. A hypotheses thereby is more general than another if its set of allowed instances is a superset to the set of instances belonging to the other hypothesis.
b. Explain Adeline Network, highlighting its advantages over Perception.
Ans. Adeline network :
- 1. ADALINE is a single linear unit, adaptive linear neuron network. The delta rule is used to train the Adaline network.
- 2. It gets input from a bias unit and numerous other units.
- 3. Trainable weights comprise an Adaline model. The weights have signs and the inputs have two possible values (+1 or -1). (positive or negative).
- 4. Weights are initially assigned at random. The output is returned to +1 or -1 by applying the net input to a quantizer transfer function (activation function).
- 5. The Adaline model compares the goal and bias units with the actual output before adjusting all the weights.
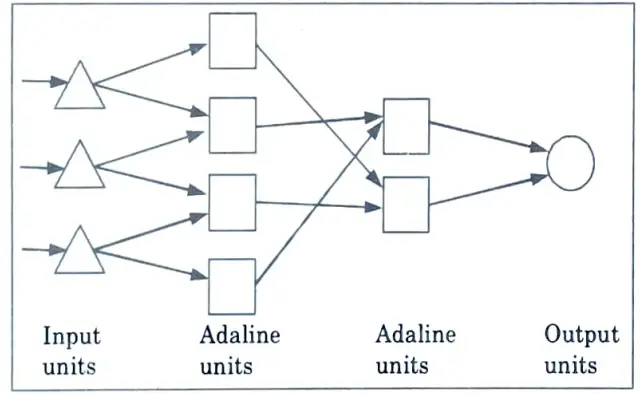


Advantages of adeline network over preception :
- 1. It uses bipolar activation function.
- 2. It uses delta rule for training to minimize the Mean-Squared Error (MSE) between the actual output and the desired/target output.
- 3. The weights and the bias are adjustable.
c. What is the assumption in Naïve Bayesian Algorithm that makes is different from Bayesian Theorem.
Ans.
- 1. Bayes theorem and Naive Bayes differ in that Bayes theorem does not presuppose conditional independence whereas Naive Bayes does.
- 2. The Naive Bayes classifier approximates the Bayes classifier by assuming that the features are independent of each other under the class rather than modelling their entire conditional distribution under the class.
- 3. A Bayes classifier is best interpreted as a decision rule.
- 4. Suppose we seek to estimate the class of an observation given a vector of features. Denote the class C and the vector of features (F1, F2,…,Fk).
- 5. Given a probability model underlying the data (that is, given the joint distribution of (C, F1, F2,…,Fk)), the Bayes classification function chooses a class by maximizing the probability of the class given the observed features:
argmaxc P(C = c |F1 = f1,…, Fk = fk)
- 6. Although the Bayes classifier seems appealing, in practice the quantity P(C = c |F1 = f1,…, Fk = fk) is very difficult to compute.
- 7. We can make it a bit easier by applying Bayes theorem and ignoring the resulting denominator, which is a constant.
- 8. Then we have the slightly better
P(C = c) P(F1 = f1,…,Fk = fk | C= c)
but this is often still intractable : lots of observations are required to estimate these conditional distributions, and this gets worse as k increases.
- 9. As a consequence, an approximation is used: we pretend
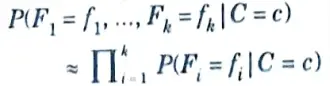
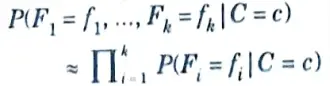
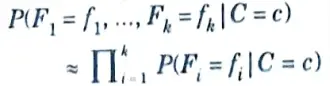
10. This is a pretty naive approximation, but in practice it works surprisingly well. Substituting this into the Bayes classifier yields the naive Bayes classifier:
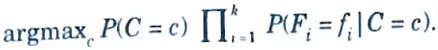
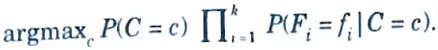
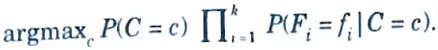
d. Differentiate between Conventional Learning and Instance based Learning.
Ans.
| S. No. | Conventional Machine Learning | Instance Based Learning |
| 1. | Train model from training data to estimate model parameters i.e., discover patterns. | Do not train model. Pattern discovery postponed until scoring query received. |
| 2. | Store the model in suitable form. | There is no model to store. |
| 3. | Generalize the rules in form of model, even before scoring instance is seen. | No generalization before scoring. Only generalize for each scoring instance individually as and when seen. |
| 4. | Predict for unseen scoring instance using model. | Predict for unseen scoring instance using training data directly. |
| 5. | Can throw away input/training data after model training. | Input/training data must be kept since each query uses part or full set of training observations. |
| 6. | Storing models generally requires less storage. | Storing training data generally requires more storage. |
| 7. | Storing for new instance is generally fast. | Storing for new instance may be slow. |
e. What are the important elements of a Reinforcement Learning Model ?
Ans. Elements of reinforcement learning :
- 1. Policy (𝛑) :
- a. It defines the behaviour of the agent which action to take in a given state to maximize the received reward in the long term.
- b. It stimulus-response rules or associations.
- c. It could be a simple lookup table or function, or need more extensive computation (for example, search).
- d. It can be probabilistic.
- 2. Reward function (r) :
- a. It defines the goal in a reinforcement learning problem, maps a state or action to a scalar number, the reward (or reinforcement).
- b. The RL agent’s sole objective is to maximise the total reward it receives in the long run.
- c. It defines good and bad events.
- d. It cannot be altered by the agent but may inform change of policy.
- e. It can be probabilistic (expected reward).
- 3. Value function (V) :
- a. Starting from that state, it specifies the overall reward that an agent can anticipate accumulating over time.
- b. A state might produce a low return but a high value (or the opposite). As an illustration, contrast instant pain or pleasure with long-term delight.
- 4. Transition model (M) :
- a. It defines the transitions in the environment action a taken in the states, will lead to state s2.
- b. It can be probabilistic.
Section 3 : S Algorithm in Machine Learning Btech
a. What are the steps involved in designing a learning system.
Ans. Steps used to design a learning system are :
- 1. Specify the learning task.
- 2. Choose a suitable set of training data to serve as the training experience.
- 3. Divide the training data into groups or classes and label accordingly.
- 4. Determine the type of knowledge representation to be learned from the training experience.
- 5. Choose a learner classifier that can generate general hypotheses from the training data.
- 6. Apply the learner classifier to test data.
- 7. Compare the performance of the system with that of an expert human.


b. Explain find-S algorithm using an example.
Ans. Working of find-S algorithm :
- 1. The process starts with initializing ‘h’ with the most specific hypothesis, generally, it is the first positive example in the data set.
- 2. We check for each positive example. If the example is negative, we will move on to the next example but if it is a positive example we will consider it for the next step.
- 3. We will check if each attribute in the example is equal to the hypothesis value.
- 4. If the value matches, then no changes are made.
- 5. If the value does not match, the value is changed to ‘?’.
- 6. We do this until we reach the last positive example in the data set.
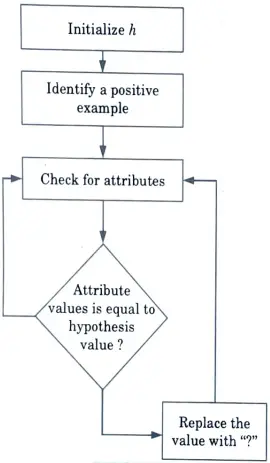


Section 4 : Decision Tree Learning in Machine Learning
a. How does Back Propagation Rule help in Learning in a Neural Network.
Ans.
- 1. The supervised learning algorithm back propagation trains multi-layer perceptrons (Artificial Neural Networks).
- 2. The programme employs a technique known as chain rule to successfully train a neural network.
- 3. The Back propagation algorithm employs a method known as the gradient descent or the delta rule to find the least value of the error function in weight space.
- 4. The weights that reduce the error function are then regarded as the learning problem’s solution.
- 5. To put it simply, back propagation makes a backward pass through a network after each forward pass while modifying the model’s parameters (weights and biases).
- 6. The gradients of the cost function with respect to those factors determine the degree of modification.
- 7. The gradients allow us to optimize the model’s parameters :
- i. Initial values of w and b are randomly chosen.
- ii. Epsilon (e) is the learning rate. It determines the gradient’s influence.
- iii. w and b are matrix representations of the weights and biases. Derivative of C in w or b can be calculated using partial derivatives of C in the individual weights or biases.
- iv. Termination condition is met once the cost. function is minimized.
b. Discuss various issue in Decision Tree Learning.
Ans. Issues related to the applications of decision trees are:
- 1. Missing data :
- a. When values have gone unrecorded, or they might be too expensive to obtain.
- b. Two problems arise :
- i. To classify an object that is missing from the test attributes.
- ii. To modify the information gain formula when examples have unknown values for the attribute.
- 2. Multi-valued attribute :
- a. The information gain measure provides an inaccurate representation of an attribute’s usefulness when it has a wide range of possible values.
- b. In the worst scenario, we might employ an attribute with a unique value for each sample.
- c. The information gain measure would then have its highest value for this feature, even though the attribute might be unimportant or meaningless, since each group of samples would then be a singleton with a distinct classification.
- d. One solution is to use the gain ratio.
- 3. Continuous and integer valued input attributes :
- a. There are an endless number of possible options for height and weight.
- b. Decision tree learning algorithms discover the split point that provides the best information gain rather than creating an endless number of branches.
- c. Finding excellent split points can be done efficiently using dynamic programming techniques, but it is still the most expensive step in practical decision tree learning applications.
- 4. Continuous-valued output attributes :
- a. A regression tree is necessary if we want to predict a number rather than discrete categories, such as the cost of an artwork.
- b. Instead of a single value at each leaf, this type of tree has a linear function of a subset of numerical properties.
- c. The learning algorithm must determine when to cease separating and to start using linear regression with the remaining attributes.
Section 5 : Bayesian Networks in Machine Learning
a. Differentiate between sample error and true error.
Ans.
| S. No. | Sample Error | True Error |
| 1. | Sample error represents the fraction of the sample which is misclassified. | The likelihood that a random sample from the population would be incorrectly classified is represented by the true error. |
| 2. | Sample error is used to estimate the errors of the sample. | True error is used to estimate the error of the population. |
| 3. | Sample error is easy to calculate. You just have to calculate the fraction of the sample that is misclassiñed. | Calculating true error is tough. On the basis of Sample error, the confidence interval range is used to estimate it. |
| 4. | Sampling error can be of type population-specific error, selection error, sample-frame error, and non-response error. | The true error can be caused by poor data collection methods, election bias, or non-response bias. |
b. Write short notes on Bayesian belief networks.
Ans.
- 1. Joint conditional probability distributions are specified by Bayesian belief networks.
- 2. They may also be referred to as belief, Bayesian, or probabilistic networks.
- 3. Class conditional independencies between groups of variables can be defined using a belief network.
- 4. It offers a graphical representation of a causal link that can be used to do learning.
- 5. A trained Bayesian network can be used for categorization.
- 6. There are two components that define a Bayesian belief network :
- a. Directed acyclic graph :
- i. Each node in a directed acyclic graph represents a random variable.
- ii. These variable may be discrete or continuous valued.
- iii. These variables may correspond to the actual attribute given in the data.
Directed acyclic graph representation: The following diagram shows a directed acyclic graph for six Boolean variables.
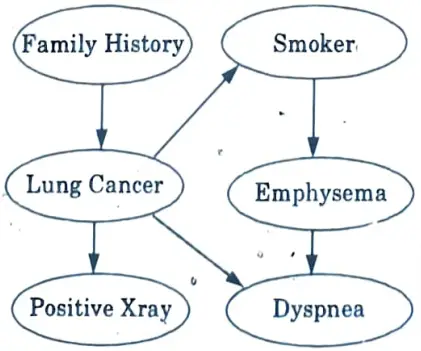


- i. The diagram’s arc enables causal knowledge to be represented.
- ii. For instance, a person’s risk of developing lung cancer depends on both whether they smoke and their family’s history of the disease.
- iii. Given that we already know the patient has lung cancer, it’s important to note that the variable Positive X-ray is unaffected by the patient’s smoking status or by whether the patient has a family history of lung cancer.
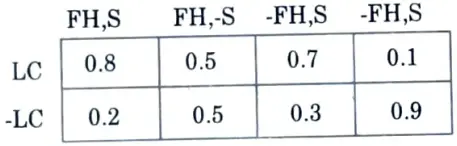
b. Conditional probability table :
The conditional probability table for the values of the variable LungCancer (LC) showing each possible combination of the values of its parent nodes, FamilyHistory (FH), and Smoker (S) is as follows :


Section 6 : Case-Based Learning in Machine Learning
a. What is Sample Complexity for Finite Hypothesis Spaces ?
Ans.
- 1. The number of training samples we must give the method to ensure that the function it returns is within an arbitrarily tiny error of the best feasible function, with probability arbitrarily near to 1, is known as sample complexity.
- 2. There are two variants of sample complexity :
- a. The weak variant fixes a particular input-output distribution.
- b. The strong variant takes the worst-case sample complexity over all input-output distributions.
- 3. There is no method that can learn the globally-optimal target function with a limited number of training samples since the strong sample complexity is infinite.
- 4. The sample complexity, however, is finite and depends linearly on the VC dimension on the class of target functions if we are only interested in a specific class of target functions (for example, only linear functions).
b. What are the Principles of a Case-based learning?
Ans. 1. Case-based learning (CBL) is an instructional design model that is a variant of project-oriented learning.
2. The principles of a case-based learning are as follows :
- A. Features :
- i. Learner-centered.
- ii. Collaboration and cooperation between the participants.
- iii. Discussion of specific situations, typically real-world examples.
- iv. Questions with no single right answer.
- B. Students :
- i. Engaged with the characters and circumstances of the story.
- ii. Identify problems as they perceive it.
- iii. Connect the meaning of the story to their own lives.
- iv. Bring their own background knowledge and principles.
- v. Raise points and questions, and defend their positions.
- vi. Formulate strategies to analyze the data and generate possible solutions.
- C. Teacher :
- i. Facilitator.
- ii. Encourages exploration of the case and consideration of the characters’ actions in light of their own decisions.
- D. Cases :
- i. Factually-based.
- ii. Complex problems written to stimulate classroom discussion and collaborative analysis.
- iii. Involves the interactive, student-centered exploration of realistic and specific situations.
Section 7 : Genetic Algorithm in Machine Learning
a. Explain the working of Q-Learning Algorithm in Reinforcement Learning.
Ans.
- 1. One of the most well-known reinforcement learning algorithms is Q learning.
- 2. Q learning is an off-policy algorithm, which means that we utilise two different policies-one for deciding on an action to take in the environment and another for determining the best course of action.
- 3. The epsilon-greedy policy and the greedy policy are the two policies utilised in Q learning.
- 4. We apply an epsilon-greedy policy to choose an action in the environment.
- 5. We employ a greedy policy when updating the Q value of the following state-action pair.
- 6. That is, we select action a in state s using the epsilon-greedy policy and move to the next state s’ and update the value using the update rule shown below :
Q(s, a) = Q(s, a) + (r + ץQ(s’, a’) – Q(s, a)
- 7. In the preceding equation, in order to compute the Q value of the next state-action pair, Q(s’, a’), we need to select an action.
- 8. Here, we select the action using the greedy policy and update theQ value of the next state-action pair.
- 9. We know that the greedy policy always selects the action that has the maximum value. So, we can modify the equation to :
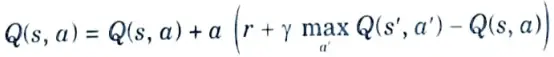
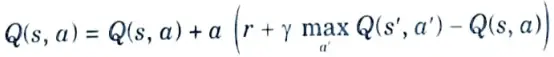
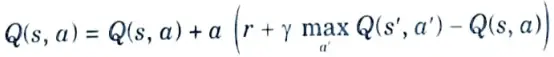
- 10. As we can observe from the preceding equation, the max operator implies that in state s’, we select the action a’ that has the maximum Q value.
- 11. The Q learning algorithm is given as follows :
- 1. Initialize a Q function Q(s, a ) with random values
- 2. For each episode :
- 1. Initialize state s
- 2. For each step in the episode :
- i. Extract a policy from Q(s, a) and select an action a to perform in state s.
- ii. Perform the action a, move to the next state s’, and observe the reward r.
- iii. Update the Q value as
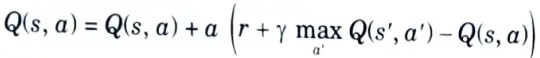
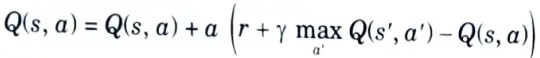
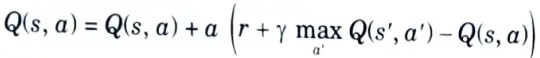
- iv. Update s = s’ (update the next state s’ to the current state s).
- v. If s is not a terminal state, repeat steps (i) to (v).
b. What are the operations involved in Hypothesis Space searching through Genetic algorithm ?
Ans. Following are the operations involved in hypothesis space searching through genetic algorithm :
- 1. A genetic algorithm’s fundamental premise is to search a hypothesis space in order to identify the optimal hypothesis.
- 2. Randomly produced starting hypotheses are gathered into a population, and each one is assessed using a fitness function.
- 3. The likelihood of selecting a hypothesis to produce the following generation is higher for those with higher fitness.
- 4. A small percentage of the finest hypotheses may be passed on to the following generation, while the others are subjected to genetic processes like crossover and mutation to produce new theories.
- 5. The population size is constant over generations.
- 6. This process is repeated until the predetermined maximum number of generations is reached or a predetermined fitness criterion is satisfied.

1 thought on “Machine Learning: AKTU Question Paper with Answer”