Discover responses on Optimization Techniques from BCA solved question papers. Use numerical techniques, linear programming, and algorithms to their full potential to effectively tackle challenging issues and excel in the classroom.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Optimization Techniques: * Important Short Questions * Solved Question Paper * Syllabus
Section A: Optimization Techniques Very Short Question Answer
Q1. Define optimal solution of a linear programming problem.
Ans. In general, the linear programming issue requires you to optimise (maximize/minimize) a linear function of variables called the objective function while keeping in mind a set of linear equations and/or linear inequations called the constraints or restrictions.
The term linear denotes that all of the relationships controlling the problem are linear, whereas programming denotes the process of developing a specific programme or plan of action.
Q2. Define deterministic model in inventory theory.
Ans. Single item a deterministic demand model assumes that the demand for an item is constant and uniform, i.e. that the values of variables are known. We presume in deterministiC models that all problem inputs, notably consumer demand, are known/certain when decisions are taken. In reality, a business must always estimate future demand using some kind of forecasting model. This forecasting model’s outputs may contain a mean demand and a standard deviation of demand. In deterministic models, however, we employed simply the mean and ignored any uncertainty information, such as the standard deviation. The resulting models are simpler, but frequently less realistic.
Q3. Define sequencing problem.
Ans. The choosing of an appropriate order for a finite number of different activities to be done on a finite number of machines is referred to as a sequencing problem. It is used to find the ideal order of executing jobs in order to decrease total time.
Q4. Explain queue length, waiting time and traffic intensity.
Ans. Queue Length: The average number of clients waiting in queue for service is referred to as queue length. If the queue is huge, it suggests that the server’s performance is poor, whereas a tiny queue shows that the server’s performance is good.
Waiting Time: The average time that a customer spends in a queue to acquire service is referred to as the waiting time in a queue. A long waiting time implies dissatisfaction and a loss of future revenue, whereas a short waiting time indicates very good service capacity.
Traffic Intensity: In telecommunication networks, traffic intensity is a measure of the average occupancy of a server or resource during a specified period of time, normally a busy hour.
Q5. Explain group replacement and individual replacement.
Ans. Group replacement policy :
- 1. Under this policy all items are replaced in a group after a particular amount of time, no matter how many items in group are failed.
- 2. Group replacement policy is uneconomical.
- 3. Group replacement is done at the time when the machine is normally non-operative.
- 4. There is cost in term of lost production.
Individual replacement policy :
- 1. Under this policy the items should be replaced right after the failure.
- 2. Individual replacement policy is economical.
- 3. Individual replacement is done where machine is operative.
- 4. There is no cost in term of lost production.
Section B: Optimization Techniques Short Question Answer
Q6. Solve the following assignment problem:
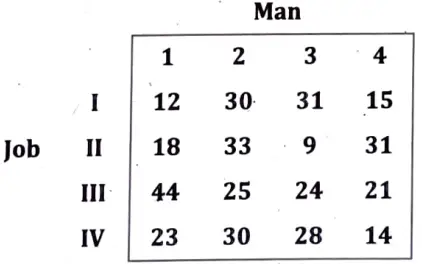


Ans. Step 1. Row Operation: Subtract minimum element of each row from every element of each row.
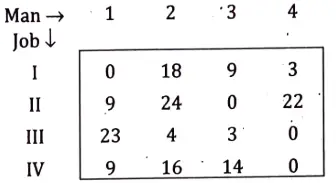


Step 2. Column Operation: Subtract minimum element of each column from every element of each column and give assignments.



Step 3. Assigning the zero ☐ in the row that have only one zero and x cross out other zero in the column. Same method is applied along column.



Q7. The cost of a machine is 6100 and its scrap value is only 100. The maintenance costs are found from experience to he as below:
| Year | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Maintenance | 100 | 250 | 400 | 600 | 900 | 1250 | 1600 | 2000 |
cost in.
When should the machine be replaced.
Ans. Given, C = Rs 6100 and S = Rs 100
Optimum replacement period is determined as below:
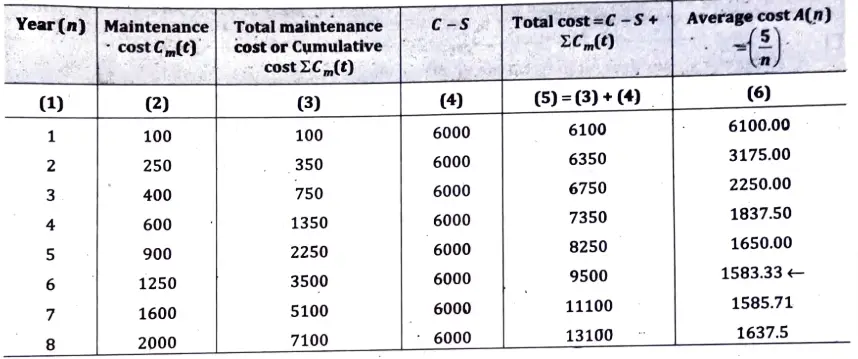


This table shows that the value A(n) during the sixth year is minimum. Hence, the machine should be replaced after every 6th year.
Q8. We have five jobs each of which must go through two machines A and B in the order AB. Processing times in hours are given in the table below:
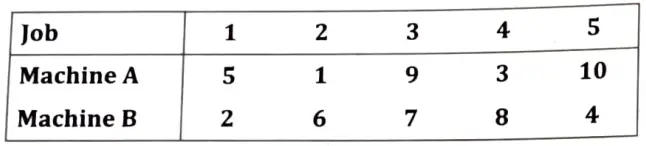


Determine the sequence for the five jobs that will minimise the ellipse time.
Ans. The minimum time in the above tables is 1, which is A2. Hence, we shall do the 2nd job first, we list the jobs as shown below:
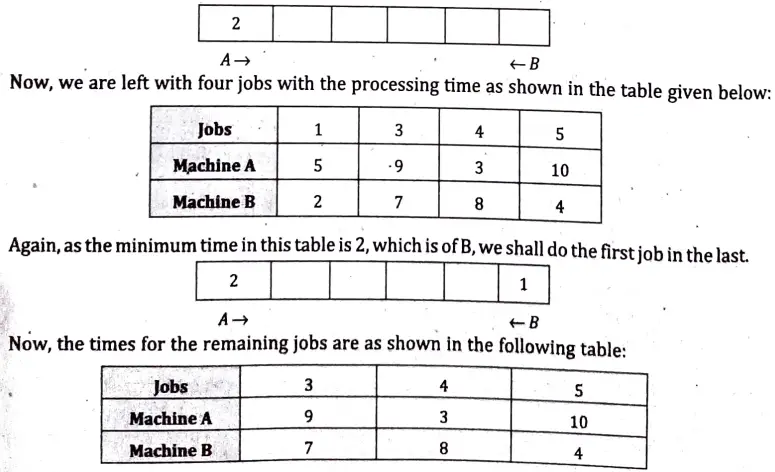


Again, as the: minimum time in this table is 3 which is of machine A and next minimum time is 4 of machine B and similarly, following the prescribed criteria, we conclude the optimal sequence of jobs as:
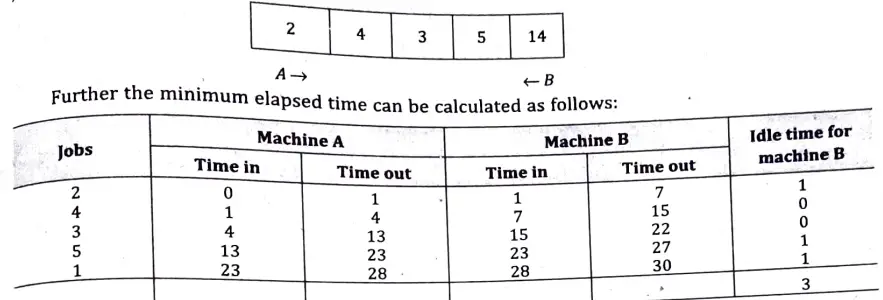


From the above table, it is clear that total time elapsed is 30 hours, idle time for machine Bis 3 hours and idle time of machine A = 30 – 28 = 2 hours.
Section C: Optimization Techniques Detailed Question Answer
Q9. Solve the following LPP:
Max. Z = 5x1 +3x2
S.t. 3x1+ 5x2 15
5x1 + 2x2 ≤ 10
x1 ≥ x2 ≥ 0
Ans. The given problem is of maximisation and all the bi‘s are non-negative. Converting the inequalities of constraints into equations by introducing slack variables x3, x4 .Also, the coefficients of slack variables are zero in the objective function. Thus, the given problem becomes :
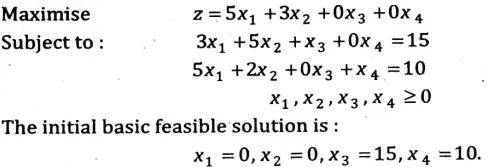
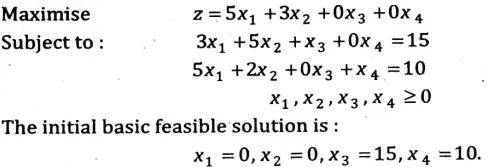
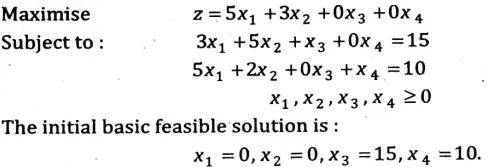
The solution to the problem using simplex method is given in the following table :
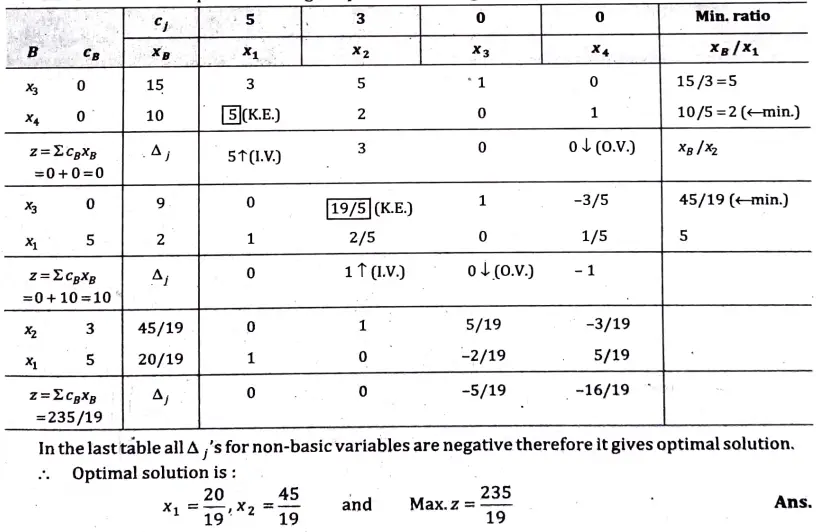


Q10. Solve the following transportation problem:
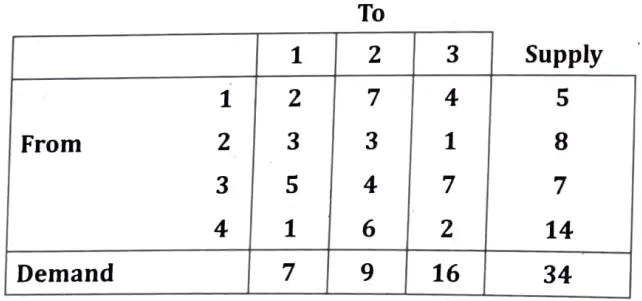


Ans. Step 1. The given transportation problem is



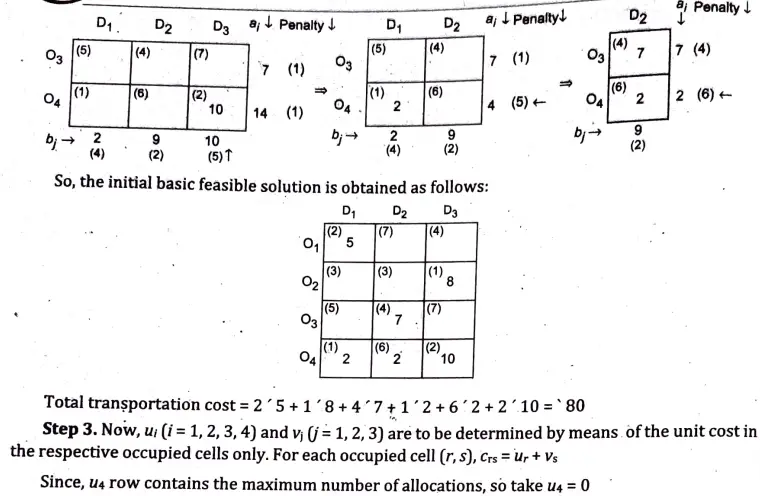





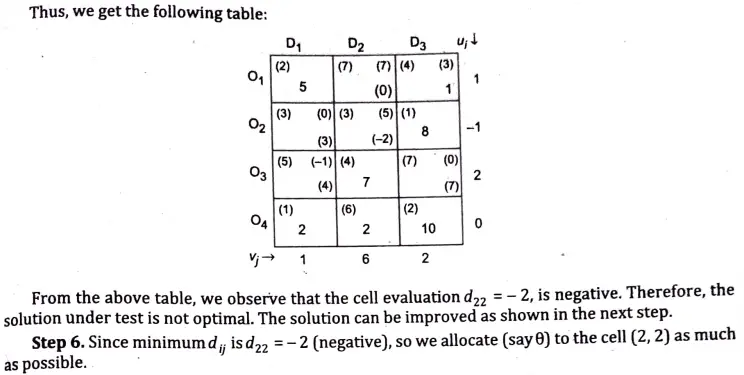





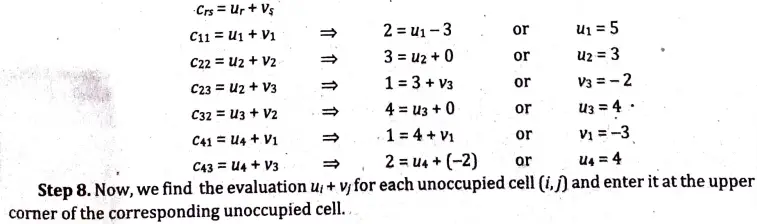
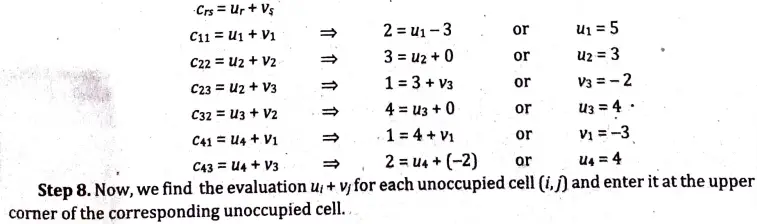
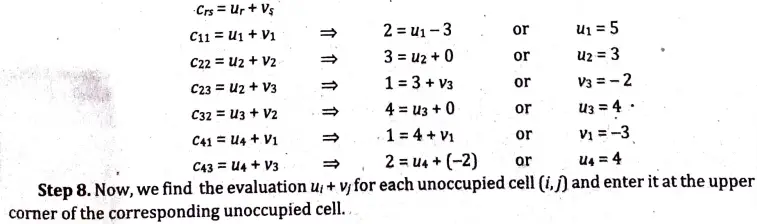






Q11. We have five jobs, each of which must go through the machines A,B and C in the order ABC, processing times are as follows:
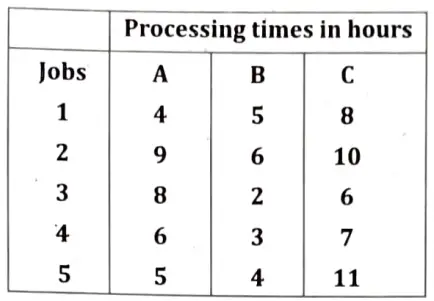


Determine a sequence for the five jobs that will minimise the elapsed time T.
Sol. Verification of Condition:
Minimum processing time on machine M1 = 6
Maximum processing time on machine M2 = 6
Minimum processing time on machine M3 = 5
Since, minimum M1 ≥ maximum M2, the required condition is satisfied.
Adding the processing times for M1 and M2 first and then M2 and M3, we get
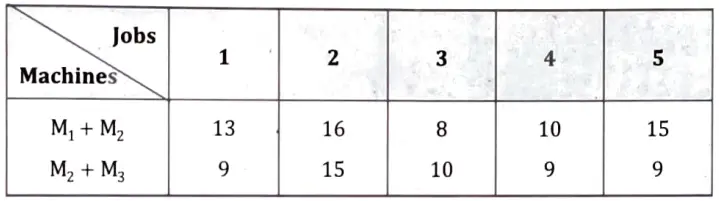


The optimum sequencing is as follows :



Calculation of Elapsed Time
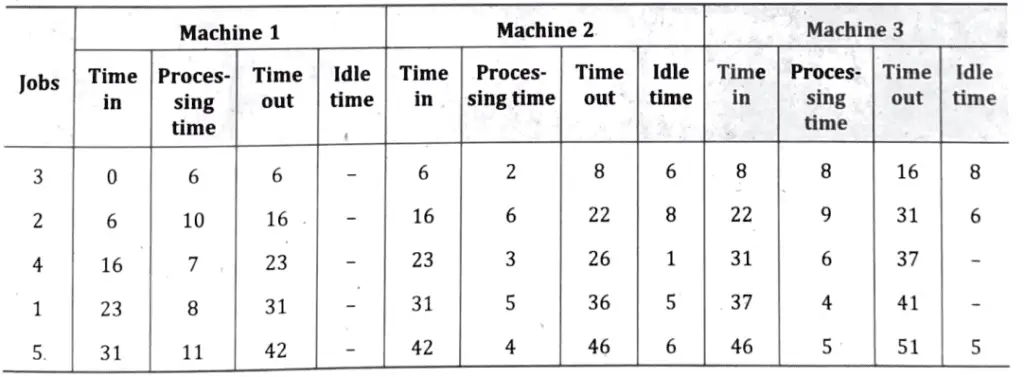


Thus, elapsed time (minimum) for sequence 3 → 2 → 4 → 1 → 5 = 51 hours.
Q12. The cost of a new machine is 5000. The maintenance cost of nth year is given by C = 500 (n-1), n = 1,2,3,…. Suppose that the discount rate per year is 0.5. After how many years it will be economical to replace the machine by new one?
Ans. Determination of.Optimal Replacement Period
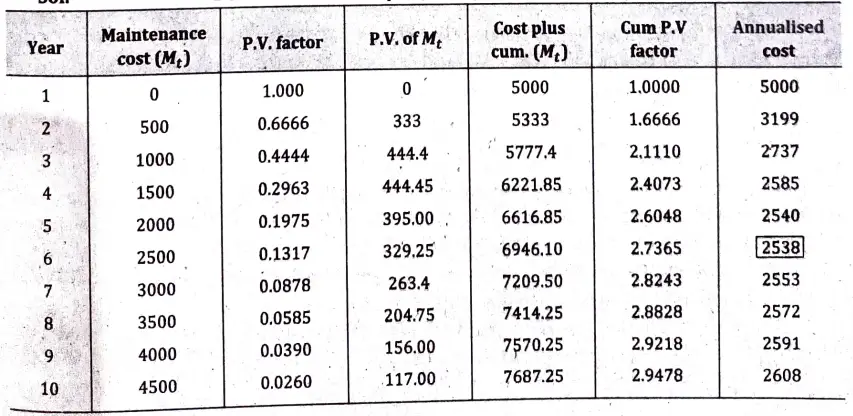


Since, the minimum annualised cost is at the sixth year and next periods maintenance cost is greater than this, the optimum replacement interval f for the machines is six years.
Q13. Customers arrive at a sales counter manned by a single person according to a poisson Process with a mean rate of 20 per hour. The time required to serve a customer has an exponential distribution with a mean of 100 seconds. Find the average waiting time of a customer and queue length.
Ans.
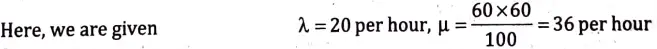
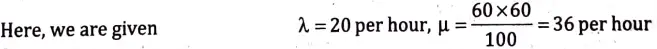
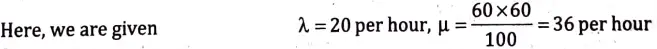
The average waiting time of a customer in the queue is given by



