Access notes on Mathematics-II from BCA solved question papers. Enhance your mathematical skills with thorough solutions to ensure success on your BCA journey.
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Mathematics-II: * Important Short Questions * Solved Question Paper * Syllabus
Section A: Mathematics-II Very Short Question Solutions
Q1. Define sets and Universal sets with example.
Sol. Set : It is a well-defined collection of objects. The objects of a set are called the elements or members of that set and their membership is defined by certain conditions.
For example;
- 1. The collection of all the letters of English alphabet a, b, c, d, …
- 2. The collection of all natural numbers denoted by N.
- 3. The collection of vowels in English alphabet.
Universal Set : When we are given a particular set and we consider different subsets of the given set, this given set is called universal set. It is denoted by U.
For example;
- 1. The universal set is the set of real numbers R, while considering the set of natural numbers, whole numbers, integers and rational numbers.
- 2. The set of alphabets is the universal set from which the letters of any word may be chosen to form a set.
- 3. In geometry, we discuss set of lines, triangles and circles, then universal set is the plane, in which the lines, triangles and circles lie.
Q2. Define equivalence Relation and show that the relation S ={(a, b) :a ≥ b} on the set R of real no is an equivalence relation.
Sol. A relation R on a set E is said to be an equivalence relation, if it is :
- (a) reflexive
- (b) symmetric, and
- (c) transitive.
Check for Reflexive:
It is given that R = {(a, b) : a ≥ b}
It is clear that (a, a) ∈R as a = a
Therefore, R is reflexive.
Check for Symmetric:
If a ≥ b, then b ≥ a.
This statement is true only for the case a=b.
Therefore, R is symmetric.
Check for Transitivity:
Now let (a, b) (b, c) ∈R
Then a ≥ b and b ≥ c
⇒ a ≥ c
⇒ (a, c) ∈R
Therefore, R is a transitive.
Hence, R is reflexive, transitive and symmetric. So, R is an equivalence relation.
Q3. Show that the inclusion relation ⊆ is a partial ordering on the power set of a set S.
Sol. Since A ⊆ A for any subset A ⊆ S, we conclude that this relation is reflexive.
Taking into account that A ⊆ B and B ⊆ A imply A = B, we conclude that the relation is antisymmetric.
Since A ⊆ B and B ⊆ C imply A ⊆ C,it follows that this relation is transitive.
Consequently the inclusion relation is a partial ordering on the power set of a set S. Ans.
Q4. If z = exy2, x = t cost, y = t sint compute dz/dt at t = 𝜋/2.
Sol. Given z = exy2
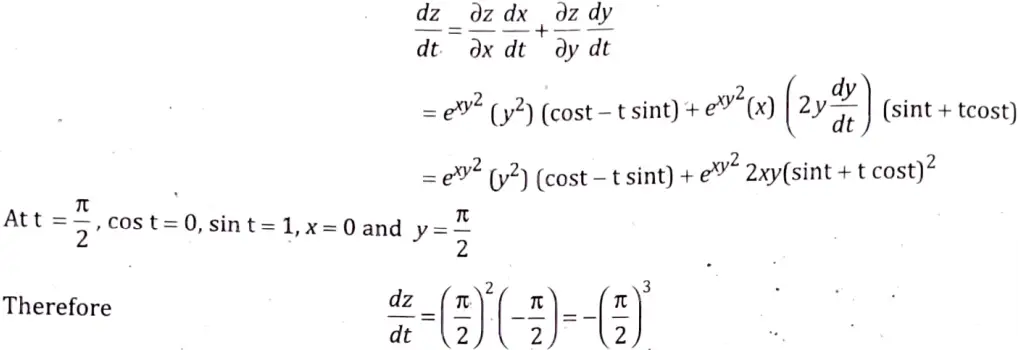
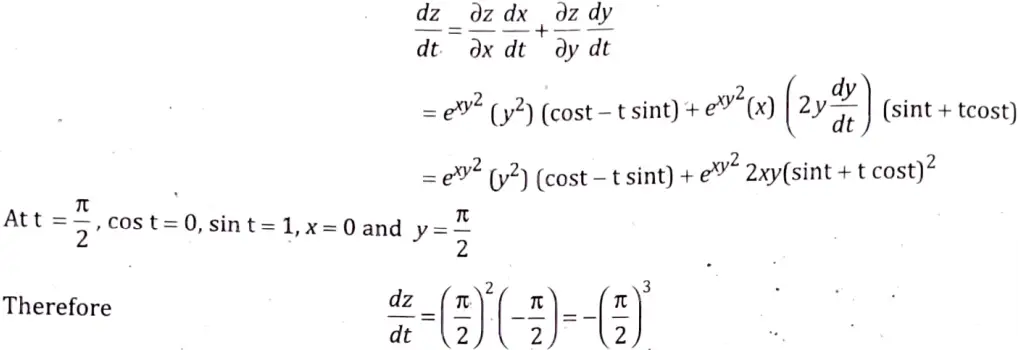
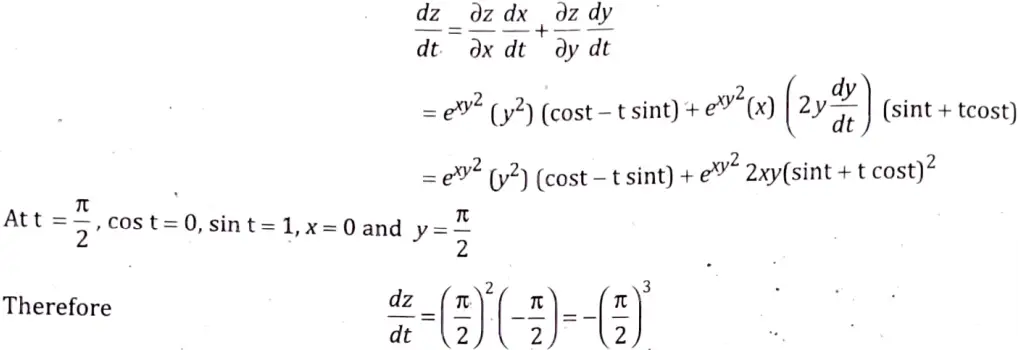
Q5. If cos α, cos β, and cos γ are the direction cosines of a straight line then prove that sin2 α + sin2 β + sin2 γ = 2.
Sol. Since cosα, cosβ, cosγ are the direction cosines of the given line, therefore
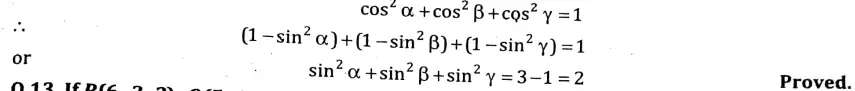
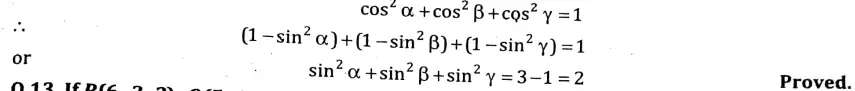
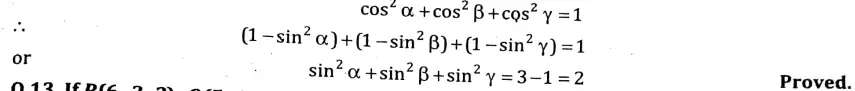
Section B: Mathematics-II Short Question Solutions
Q6. Show that Dual of a complemented lattice is complemented.
Sol. Let(L, R) be a complemented lattice with 0 and 1 as least and greatest elements. Let (L, R(bar)) be the dual of(L, R) Then 1 and 0 are least and greatest elements of (L, R(bar)).
Let a 𝛜 L be any element.
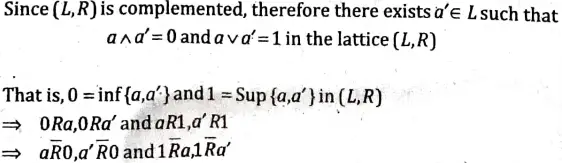
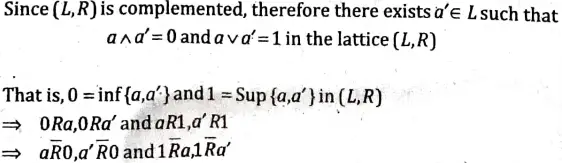
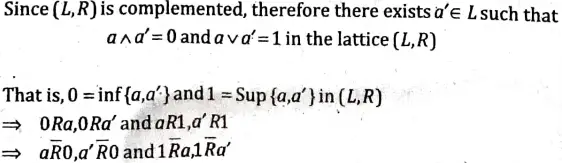
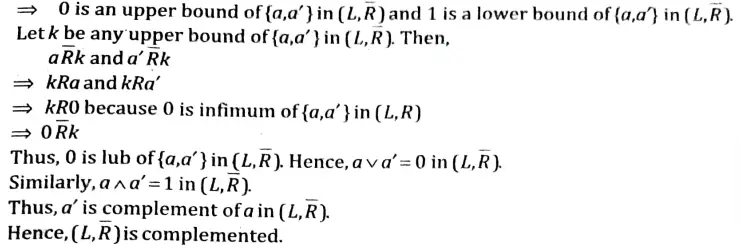
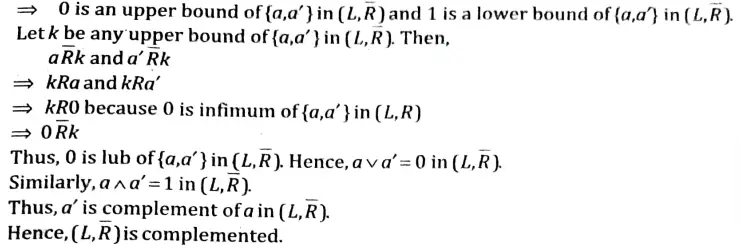
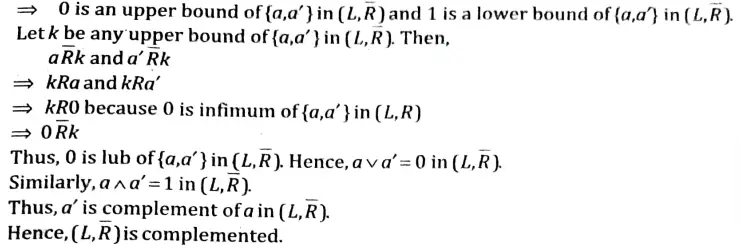
Q7. Find the equations of the straight line drawn through the origin which will intersect both the lines.
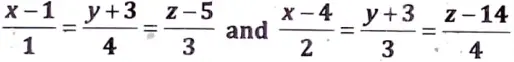
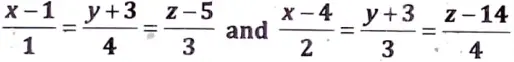
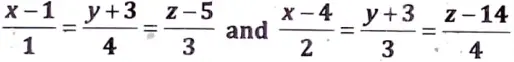
Sol. We need to find the equation of line which intersects the lines



and passes through (0, 0, 0).
Now,
Equation of line passing through two points (x1,y1, z1) and (x2, y2, z2),
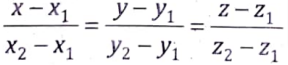
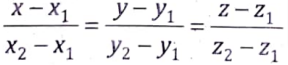
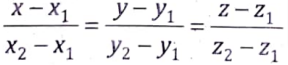
We use (x1,y1, z1) = (0, 0, 0)
Now, if point (x2, y2, z2) lies on (L1)
then
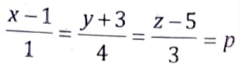
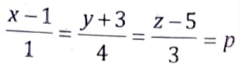
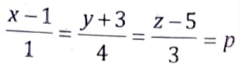
⇒ x = p + 1, y = 4p – 3, z = 3p + 5
So, (x2, y2, z2) = (p + 1, 4p – 3, 3p + 5)
Thus, the equation of lines will be
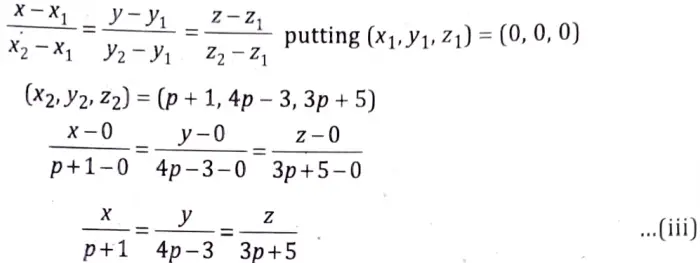
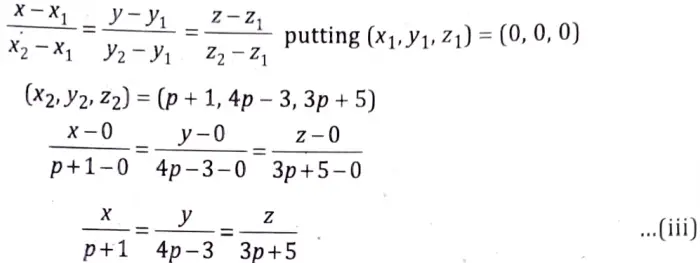
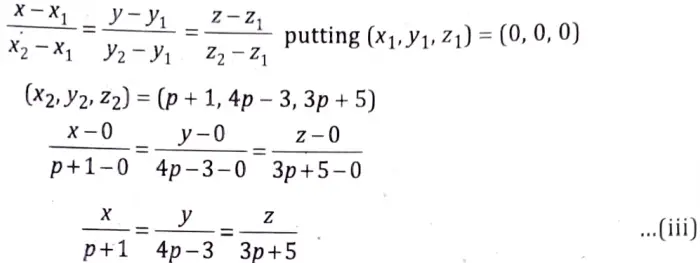
Now, if the point (x2, y2, z2) lies on (L2)
then,
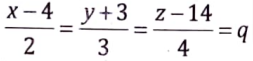
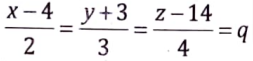
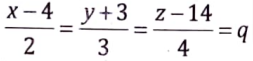
⇒ x = 2q + 4, y = 3q – 3, z = 4q + 14
So, (x2, y2, z2) = (2q + 4, 3q – 3, 4q + 14)
Then the equation of line will be
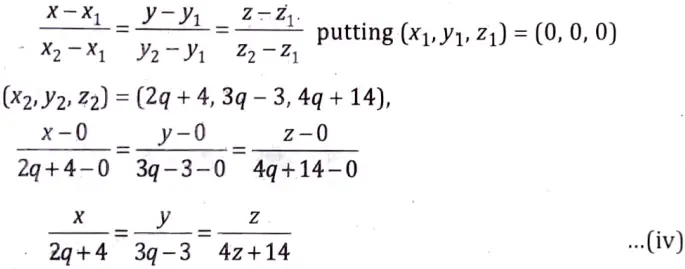
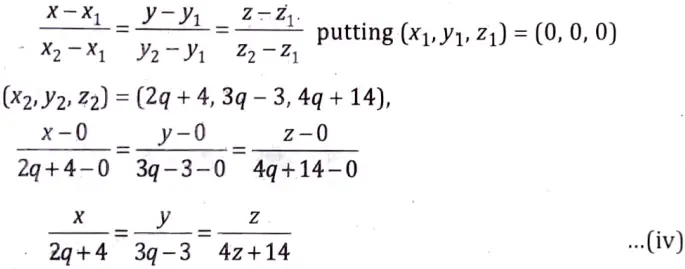
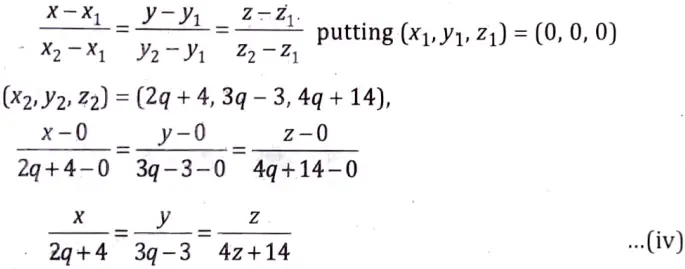
Since, the eqs. (iii) and (iv) represents the same line, so the direction ratios of lines are proportional.
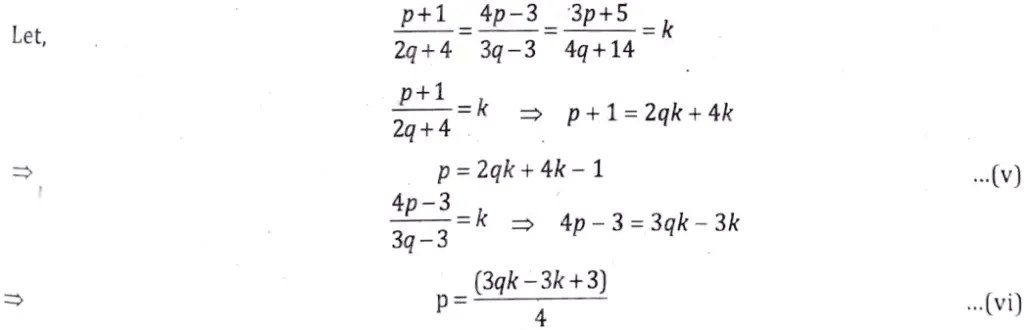
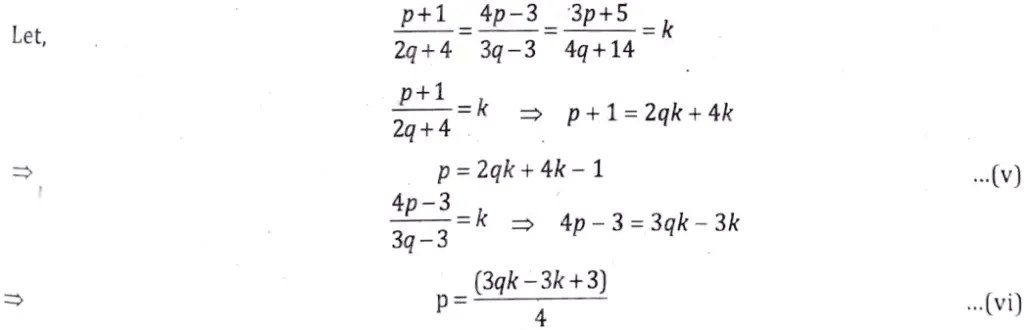
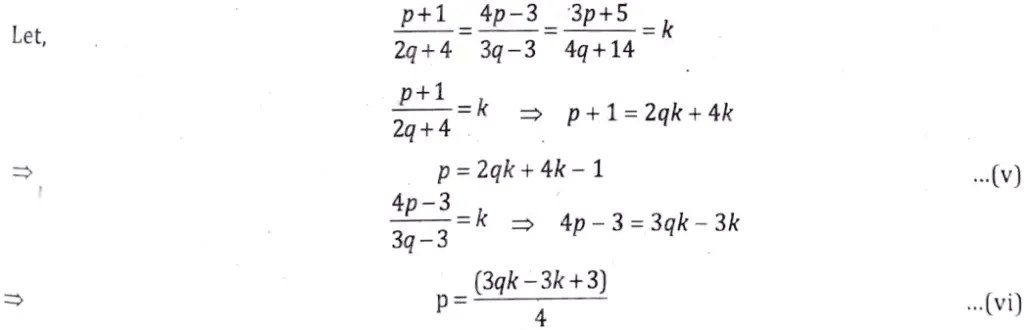
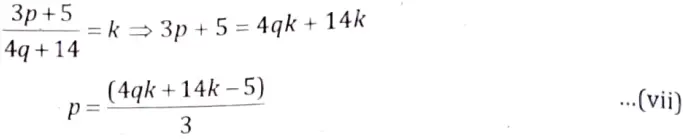
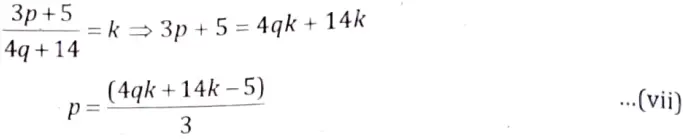
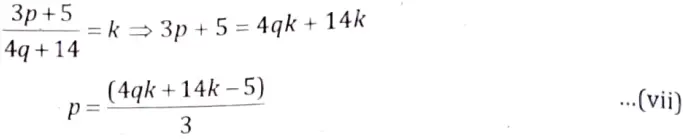
Comparing eqs. (v) and (vi),
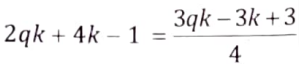
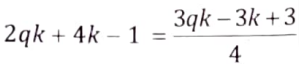
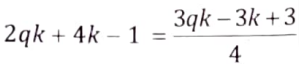
8qk + 16k – 4 = 3qk – 3k + 3
5qk + 19k = 7



Comparing eqs. (vi) and (vii),
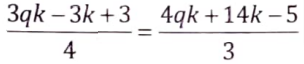
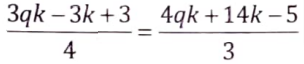
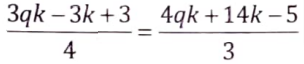
9qk – 9k + 9= 16qk + 56k – 20
7qk + 65 k = 29
k(7q + 65) = 29



From eqs. (vii) and (ix),
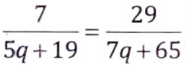
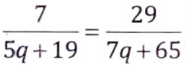
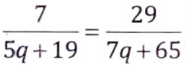
7 (7q + 65) = (5q + 19) 29
49q + 455 = 145 q + 551
96 q = -96
⇒ q = -1
Now, putting the value of q in eq. (iv),
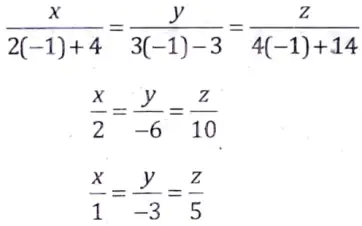
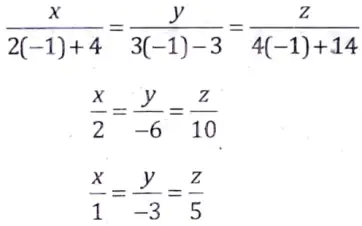
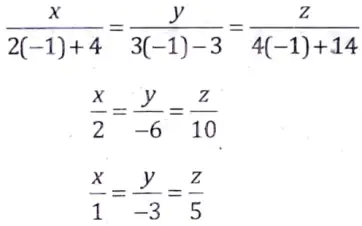
Q8. Show that f(x, y, z) =(x + y + z) – 3(x + y + 2)- 24xyz + a3 has maxima at (-1, – 1, -1).
Sol. f(x, y, z) = (x + y + z)3 – 3(x + y + z)- 24 xyz + a3
Differentiation offw.rtx,y and z,
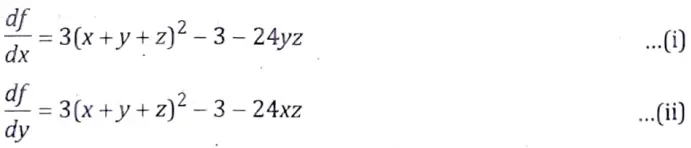
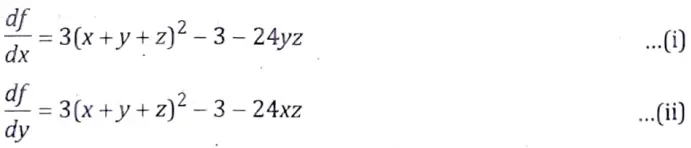
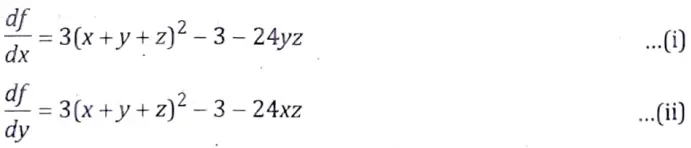
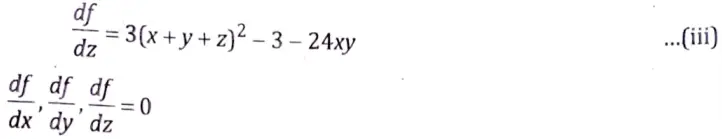
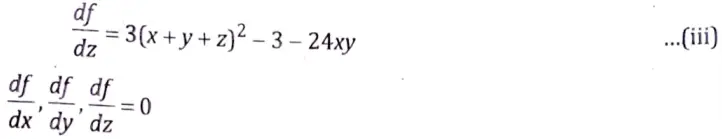
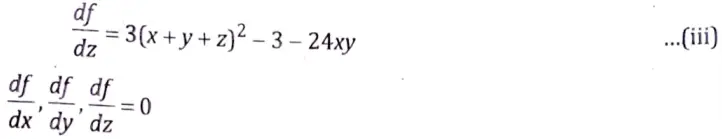
3(x + y + z)2 – 3- 24yz = 0
3(x + y + z)2 = 3 + 24yz
(x + y + z)=1 + 8yz …(iv)
and 3(x + y + z)2 – 3 – 24xz = 0
3(x + y + z) = 3 + 24xz
(x + y + z)2 = 1 + 8xz …(v)
and 3(x + y +z)2 – 3 – 24xy = 0
3(x + y + z)2 = 3 + 24xy
(x + y + z) = 3 + 24xy
(x + y + z) = 1 + 8xy …(vi)
From eqs. (iv), (v) and (vi)
1 + 8yz = 1 + 8xz = 1 + 8xy
⇒ x = y = z putting in eq. (iv)
(x + x + x) = 1 + 8xx
(3x)2 = 1 + 8x2
9x2 = 1 + 8x² ⇒ x2 = 1
⇒ x = ± 1
⇒ (x, y, z) = ± (1, 1, 1)
Again,
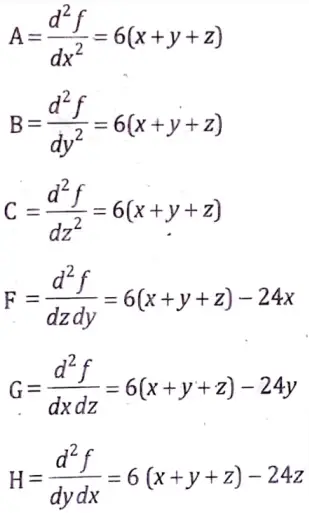
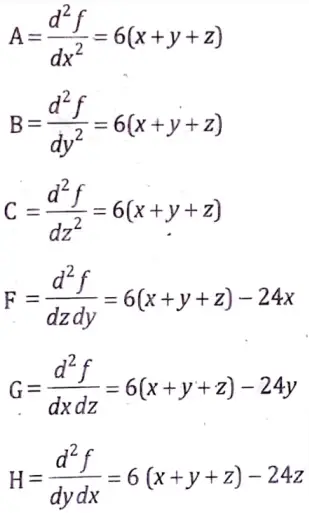
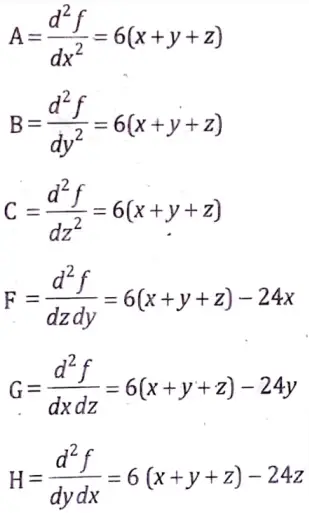
At point (-1, -1, -1),
A = – 18, B = – 18, C = – 18
F = 6, G = 6, H = 6
(1) A = – 18 < 0
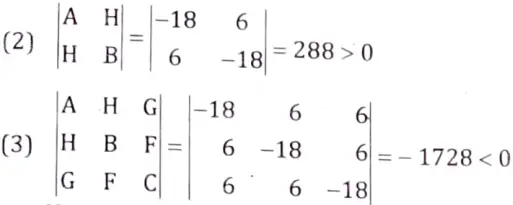
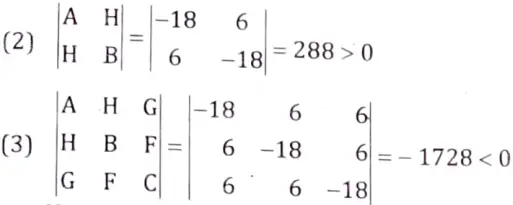
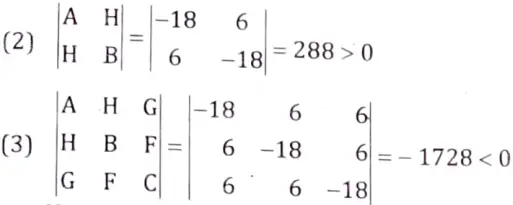
Hence f is maximum at (- 1, – 1,- 1).
Section C: Mathematics-II Detailed Question Solutions
Q9. Let the function f : R → R and g : R → R be defined by f(x) = 2x, g(x) = x2 + 2 ∀x ∈R.
(a) Check the function f and g for being.
(i) One-to-One (ii) Onto
Sol. (1) Given that f(x) = 2x
Checkf is one-one: Let x1, x2 ∈R
Now, f(x) = f(x)
⇒ 2x1 = 2x2
⇒ x1 = x2
Therefore, f is one-one
Check g is one-one: Given that g (x) = x2 + 2
Let x1, x2 ∈R
Now, g(x1) = g(x2)
⇒ x12 +2 = x22 + 2
⇒ x21 = x22
⇒ x21 – x22 = 0
⇒ (x1 – x2) (x1 + x2) = 0
⇒ x1 = ± x2
Therefore, g(x1) = g(x2) does not implies that x1 = x2
Therefore, g is not one- one.
Eg. g(-1) = 1 + 2 = 3
g(1) = 1 + 2 = 3
g(- 1) = g(1)
but – 1 ≠ 1.
(ii) Check f is onto:
Let C ∈ R, f(x) = 2x
⇒ f(x) = C
⇒ 2x= C
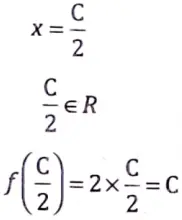
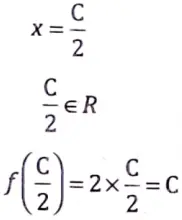
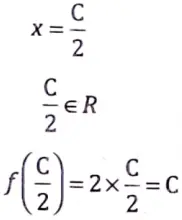
which implies that C is the image of C/2.
∴ f is onto.
Check g is onto: g(x) = x2 + 2
Let g(x) = C, such that C ∈ R



Note that Cis a real number, it can be negative also.
Putting C = – 2
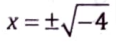
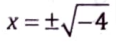
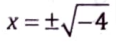
which is not possible as root of negative number is not real.
Hence x is not real.
So, y is not onto.
(b) Find the formula defining the function fog and gof and obtain the values of (fog) (2) and (gof) (1).
Sol. Composition of function:
Let f: A → B and y : B → C be two real valued functions. Then the composition of f and g denoted by gof, such that gof: A → C is defined by
(gof) (x) =g (f(x))
This is also known as function of a function or resultant of a function.
Similarly, (fog) (x) =f(g(x))
Since we have f(x) = 2x and g(x) = x2 + 2
Now, fog(x) =f(g(x)) = f(x2 + 2) = 2(x2 + 2)
fog (x) = 2(x2 + 2)
fog (2) = 2(22 + 2) = 2(4 + 2) = 12
and gof (x) = g(f (x)) = g(2x) = (2x)2 + 2 = 4x2 + 2
gof (x) = 4x2 +2
gof (1) = 4(1)2 + 2 = 4 + 2 = 6.
Q10. (a) If (L, < ) is a lattice and a, b, c and d ∈ L then.
(i) a ≤ b, c ≤ d ⇒ a ∧ c ≤ b ∧ d
(ii) a ∧ (b v c) ≥ (a ∧ b) v (a ∧ c)
Sol. (i) Since a ∧ c ≤ a and a ∧ c ≤ c,
therefore, again by transitivity
a ∧ c ≤ b and a ∧ c ≤ d (∵ a ≤ b, and c ≤ d).
⇒ a ∧ c is a lower bound of b and d.
But since b ∧ d is the g.l.b of b and d,
therefore, we have a ∧ c ≤ b ∧ d.
(ii) We know that
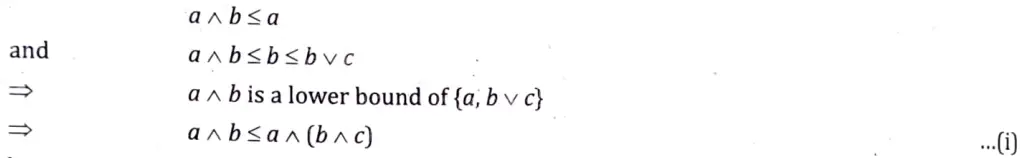
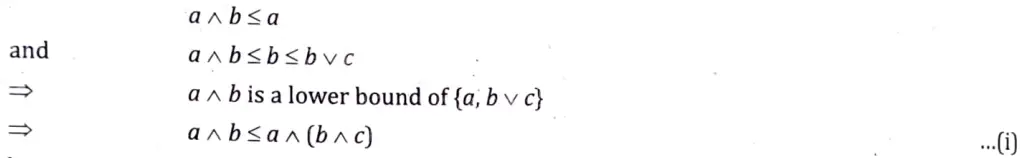
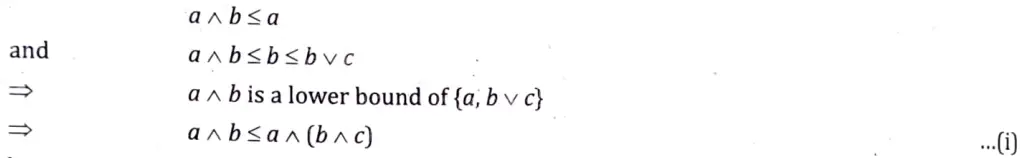
because a ∧ (b v c) is the greatest lower bound of {a, b v c}



(b) Show that dual of a lattice is a lattice.
Sol. Let (L, R) be a given lattice and let (L, R(bar)) be its dual, where R(bar) is defined as x R(bar)y if yRx. Then, it can be shown easily that (L, R(bar)) is a poset.
Let x v y = sup {x, y} in (L, R). Then we have x R(x v y) and y R (x v y)
(x v y) R(bar)x and (x v y) R(bar)y
= x v y is a lower bound of {x, y} in (L, R(bar))
Now, we will show that x v y is the greatest lower bound of {x, y} in (L, R(bar)).
Let z be any lower bound of (x, y) in (L, R(bar)), then z R(bar)x and z R(bar)y.
⇒ x R z and y R z
⇒ z is an upper bound of {x, y} in (L, R)
⇒ (x v y) Rz as x v y = sup {x, y} in (L, R)
⇒ z R(x v y)
⇒ x v y is the greatest lower bound of (x, y) in (L, R(bar)).
Similarly, it can be shown that x ∧ y is the least upper bound in (L, R(bar)).
Therefore (L, R(bar)) is a lattice.
11. (a) Show that f(x, y, z – 2x) = 0, satisfies under suitable conditions, the equation
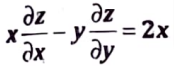
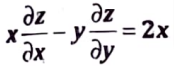
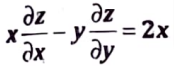
What are these conditions.
Sol. Let u = xy, V = 2 – 2x, then,
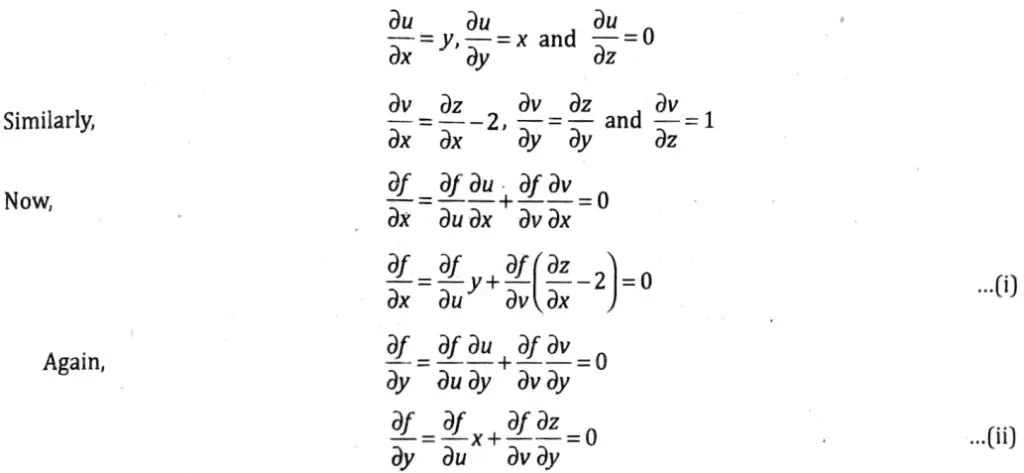
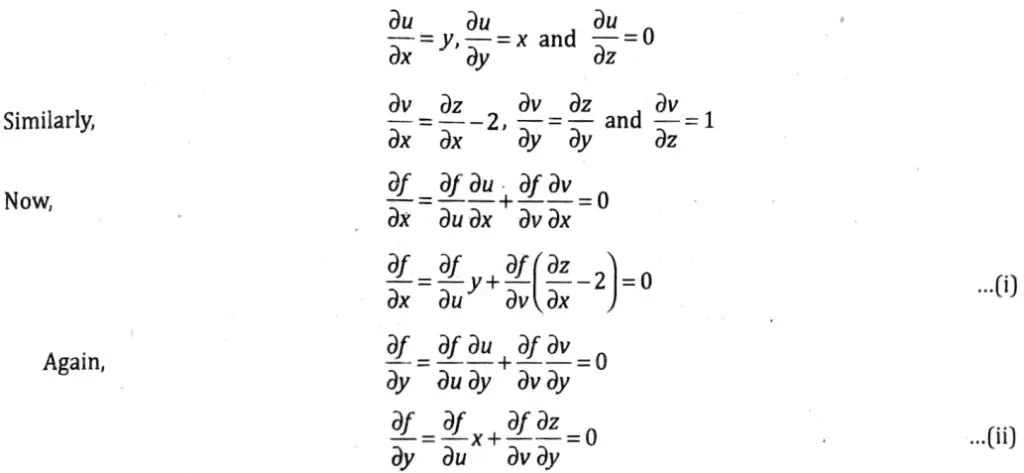
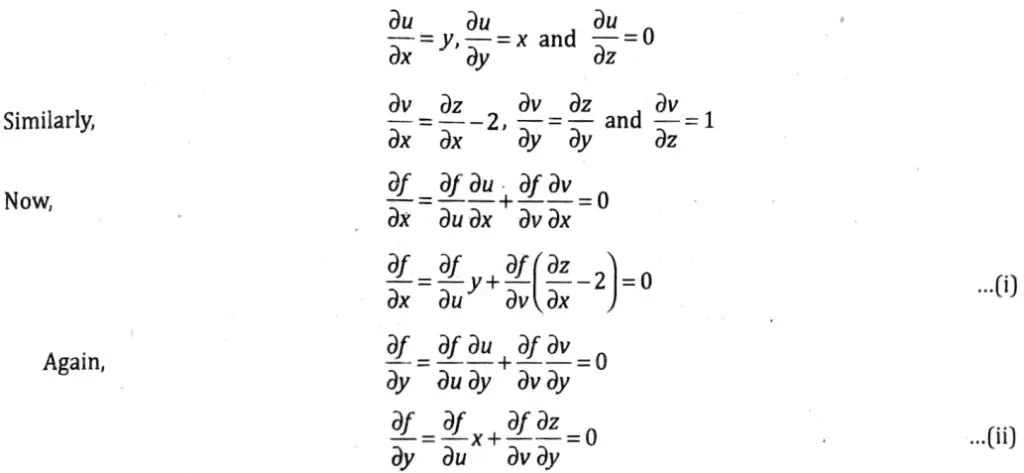
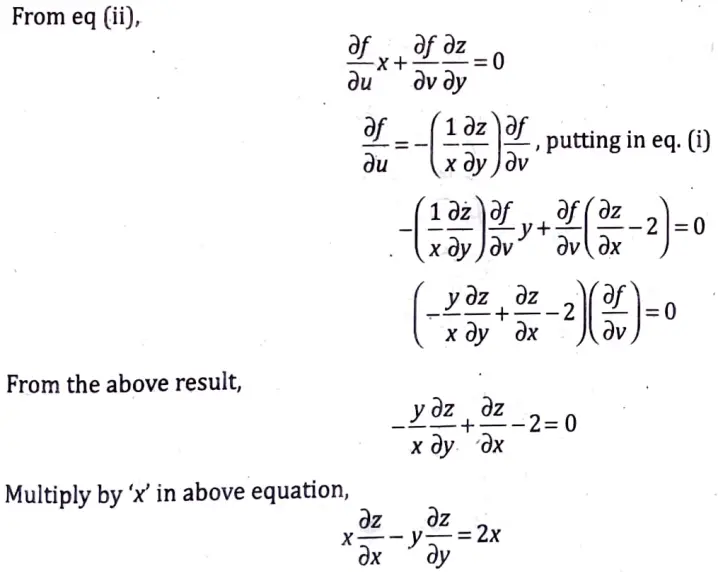
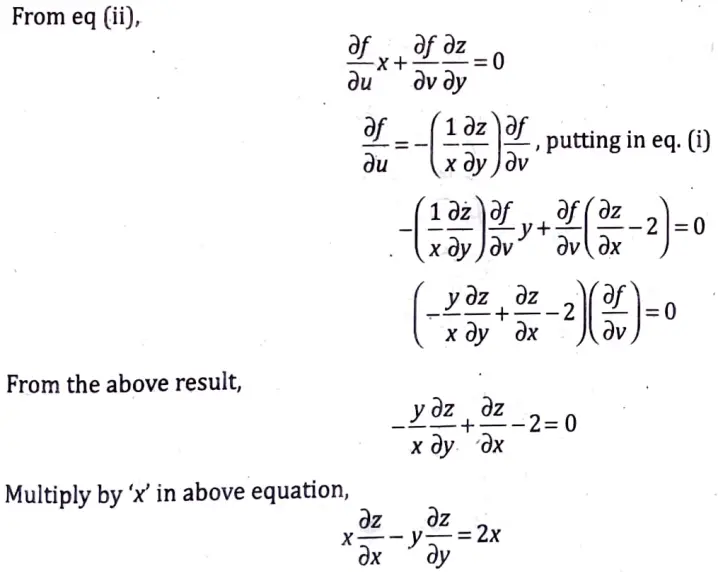
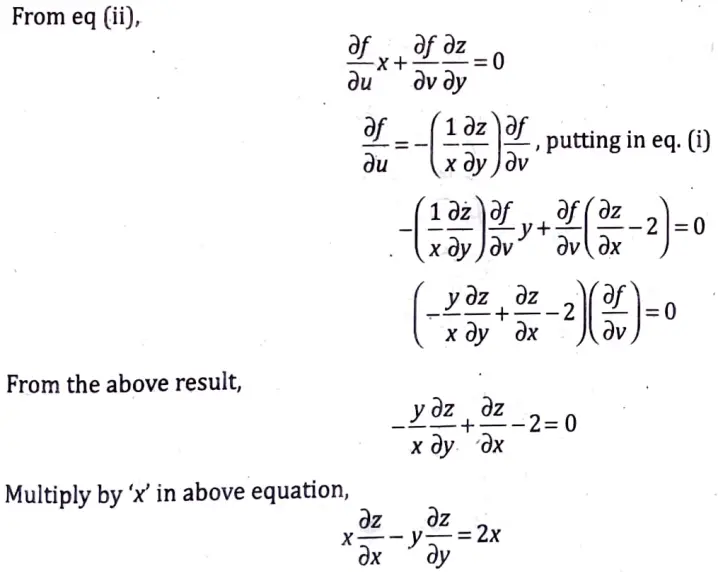
12. (a) Find the equations of the plane parallel to the plane 2x – 3y – 5z + 1 = 0 and distant 5 units from the point (- 1, 3, 1).
Sol. A plane parallel to the plane 2x – 3y – 5z + 1 =0
can be written as
2x – 3y – 5z + 𝛌 = 0
where 𝛌 is a scalar quantity.
Now distance of plane (in eq. (i)) from the point (- 1,3, 1)
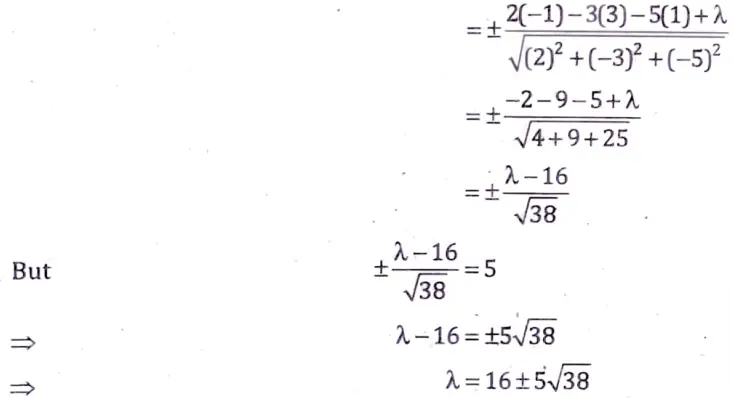
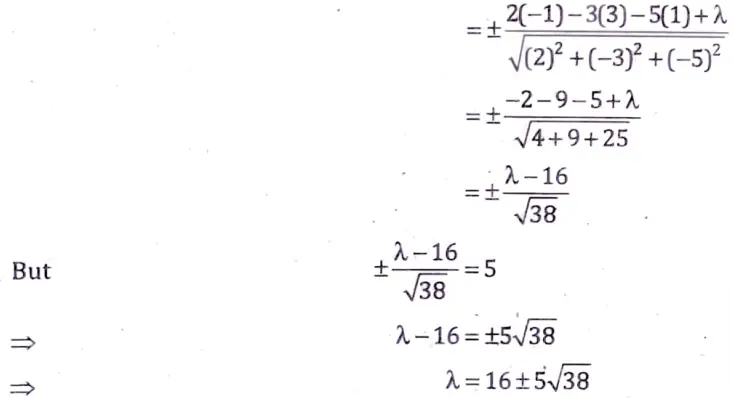
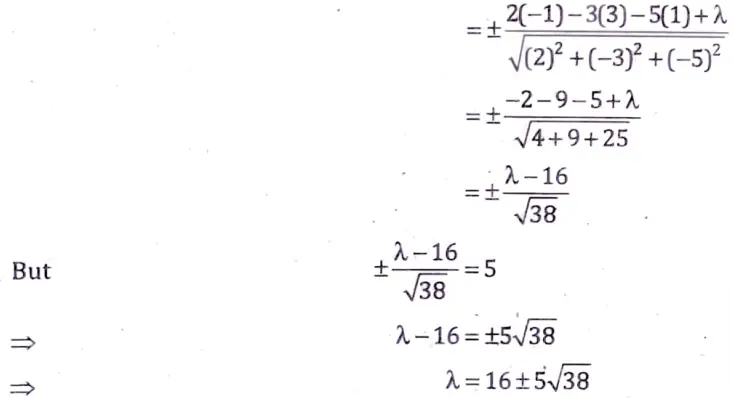
Substituting the values of 𝛌 in eq. (i),
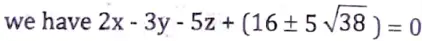
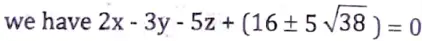
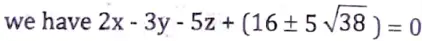
Hence, these are the equations of required planes.
(b) Find the equation of the sphere which touches the sphere x2 + y2 + z2 + 2x – 6y + 1 = 0 at (1, 2, -2) and passes through the point (1, – 1, 0).
Sol. x2 + y2 + z2 + 2x – 6y + 1 = 0
Equation of tangent plane to the sphere at (1, 2, – 2)
S1 : xx1 + yy1 + zz1 + u(x + x1) + w(y + y1) + v(z2 + z1) + d = 0
S : x2 + y2 + z2 + 2ux + 2wy + 2vz + d = 0
2u = 2, 2w = -6, 2v = 0
u = 1, w = -3, v = 0
S1= 1x + 2y – 2z + 1 (x + 1) + (-3) (y + 2) + 0 + 1 = 0
S1 = 2x + 2y – 2z +1 – 6 – 3y + 1 = 0
= 2x – y – 2z – 4 = 0
Equation of sphere = S + 𝜋 S1 = 0
= (x2 + y2 + z2 + 2x – 6y + 1) + 𝜋 (2x – y – 2z + 4) = 0
Passing through (1, -1),
⇒ (1 +1+0 + 2 +6 + 1) + 𝜋(2 +1-0+4) = 0
⇒ 11 + 7𝜋 = 0



Equation of sphere
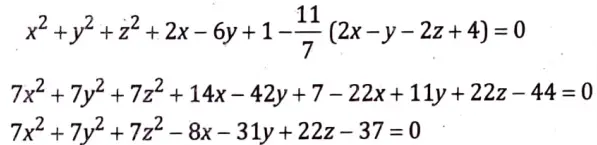
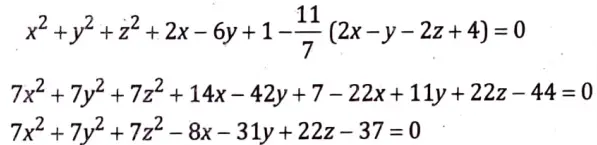
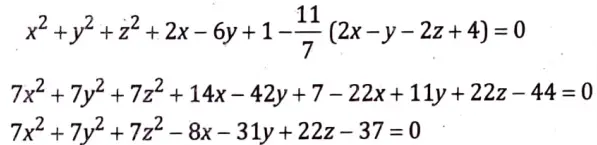
13. (b) Evaluate the following integrals by first converting to Polar coordinates.
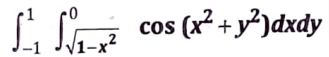
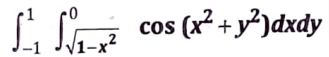
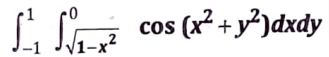
Sol. The given double integral
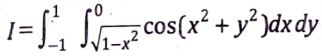
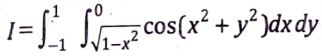
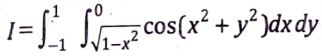
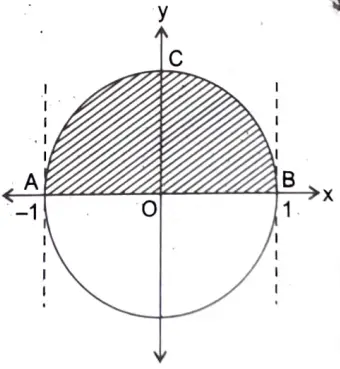


From the limits of integration it is obvious that the region of integration R is bounded by
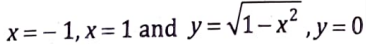
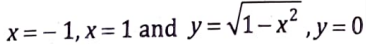
i.e. the region of integration is the area AOBCA of the circle x2 + y2 – 1 = 0 bounded by the lines x = -1 and x = 1.
Putting x = r cos 𝛉,y = r sin 𝛉 the corresponding pol¡r equation of the circle is r2 (cos2𝛉 + sin2𝛉) = 1.
Now, r2 = 1 ⇒ r = 1
Thus, r varies from r = 0 to r = 1 and 𝛉 varies from 𝛉 = 0° to 𝛉 = 𝜋. Also the polar equivalent of dx dy is rd𝛉dr.
Hence, the transformation to polar coordinates,
we have



