Everyone is welcome to our blog! Examine the field of Application of Soft Computing by taking brief notes on a test paper. Learn about important topics such as computing applications. To discover more about the intriguing field of quantum mechanics, go to Bachelorexam.com. Join us on this educational adventure!
Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well. Important Questions For Application of Soft Computing: *Quantum *B.tech-Syllabus *Circulars *B.tech AKTU RESULT * Btech 3rd Year
Section A: Application of Soft Computing Quantum Pdf
a. Define Soft Computing. How is it different from conventional computing ?
Ans. Soft Computing: Soft computing is a set of computational techniques used in computer science, machine learning, and some engineering fields to explore, simulate, and analyse extremely complicated phenomena.
Difference:
| S. No. | Soft computing | Hard (Conventional) computing |
| 1. | Soft computing is liberal of imprecision, uncertainty, partial truth and approximation. | Hard computing requires a precisely state analytic model. |
| 2. | Soft computing is based on fuzzy logic, neural sets, and probabilistic reasoning | Hard computing is based on binary logic, crisp system, numerical analysis and crisp software. |
| 3. | Soft computing will emerge its own programs. | Hard computing requires programs to be written |
b. What is difference between auto associative memory and hetero associative memory ?
Ans.
| S. No. | Autoassociative Memory | Heteroassociative Memory |
| 1. | In autoassociative memory, the associated pattern pair (x, y) is same. | In heteroassociative memory, the associated pattern pair (x, y) is different. |
| 2. | In this model, given a distorted or a partial input pattern x as input, the whole pattern with perfect form y is recalled as output. | This model recalls output y on a given input x or vice-versa. |
| 3. | Useful for image refinement. | Useful for the ass0ciation of patterns. |
c. Write down the applications of genetic algorithm.
Ans. Application of GA:
- 1. Optimization: Genetic Algorithms are most typically utilized in optimisation issues where we must maximize or reduce a certain objective function value while adhering to a set of restrictions.
- 2. Economics: GAs are also used to characterize economic models such as the cobweb model, game theory equilibrium resolution, asset pricing, and so on.
- 3. Neural networks: GAs are also used to train neural networks, particularly recurrent neural networks.
- 4. Parallelization: GAs have very good parallel capabilities and have proven to be very effective means of tackling specific issues, as well as being a valuable study area.
- 5. Image processing: GAs are also employed in digital image processing (DIP) activities such as dense pixel matching.
- 6. Machine learning: Genetics based machine learning (GBML) is a nice area in machine learning.
- 7. Robot trajectory generation: GAs have been used to plan the path that a robot arm will take as it moves from one location to another.
d. What is a self organizing map?
Ans. A self-organizing map (SOM) is a form of artificial neural network that builds a two-dimensional map of a problem space via unsupervised learning.
e. What is a membership function in a fuzzy set ?
Ans. 1. A membership function for a fuzzy set A on the universe of discourse X is defined as 𝛍A :X → [0,1], where each element of X is mapped to a value between 0 and 1.
2. This value, called membership value or degree of membership, quantifies the grade of membership of the element in X to the fuzzy set A.
3. Whether the elements in fuzzy sets are discrete or continuous, membership functions characterize fuzziness (i.e., all the information in the fuzzy set).
4. Membership functions are a way for solving practical problems based on experience rather than knowledge.
5. Graphical forms are used to depict membership functions.
f. If A(bar) = {1/1, 0.7/1.5, 0.2/2, 0.6/2.5} and B(bar) = {0.2/1, 0.3/1.5, 0.7/2, 0.1/2.5}. Find the Algebraic sum of the given fuzzy sets.
Ans.



g. What are the basic components of ANN?
Ans. ANN consists of three components:
- a. Input layer
- b. Hidden layer
- c. Output layer
h. What is meant by threshold logic unit?
Ans. The Threshold Logic Unit (TILU) is a simple machine learning model that consists of a single input unit (and associated weights) and an activation function.
i. Why do we use bias function in neural network?
Ans. Bias is analogous to an intercept in a linear equation. It is an additional parameter in the Neural Network that is used to change the output in addition to the weighted sum of the neuron’s inputs. By adding a constant to the input, we can alter the activation function.
j. What is adaptive learning ?
Ans. Adaptive learning, also known as adaptable teaching, is an educational strategy that orchestrates the interaction with the learner and delivers customised resources and learning activities to match the specific needs of each student.
Section B: Application of Computing Aktu Pdf
a. How crossover used in a GA? Explain the types of crossover with example.
Ans. Crossover operator:
- a. The crossover operator is used to the mating pool in the intention of producing a superior string.
- b. The crossover operator’s goal is to search the parameter space.
- c. Furthermore, search should be performed in such a way that the information stored in the current string is kept as much as possible because these parent strings are examples of good strings selected during reproduction.
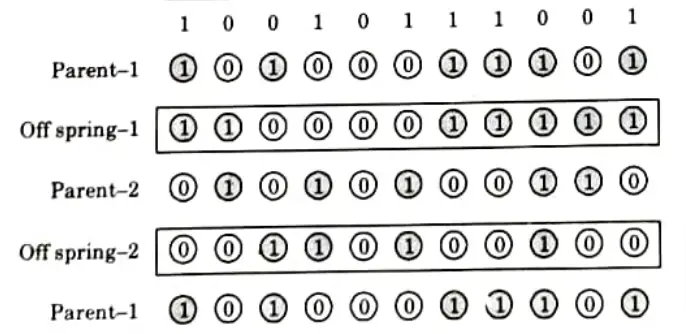
1. Single-site Crossover:
- i. In a single-site crossover, a cross-gite is selected randomly along the length of the mated strings and bits next to the cross-sites are exchanged as shown in Fig.
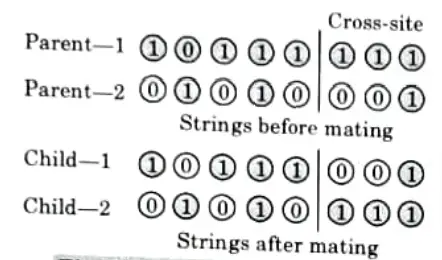


- ii. By combining beneficial chemicals from both parents, better children can be obtained if an appropriate place is picked.
- iii. Because the relevant site is unknown and is chosen at random, this random selection of cross-sites may result in enhanced children if the chosen site is appropriate. Otherwise, the string quality may suffer.
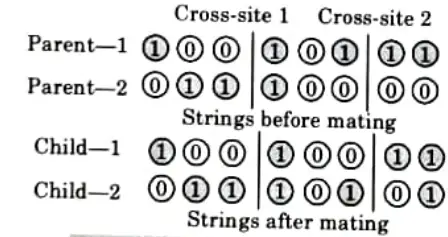
2. Two-point Crossover:
- i. A two-point crossover operator selects two random sites and exchanges the contents bracketed by these sites between two mated parents.
- ii. If the cross-site 1 is three and cross-site 2 is six, the strings between three and six are exchanged as shown in Fig.


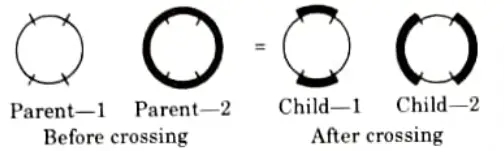
3. Multi-point Crossover:
- i. There are two possibilities in a multi-point crossover.
- ii. One is an even number of cross-sites, whereas the other is an odd number of cross-sites.
- iii. For even-numbered cross-sites, the string is considered as a ring with no beginning and no end.
- iv. The cross-sites are chosen at random around the circle.
- v. Now the information between alternate pairs of sites is interchanged as shown in Fig.


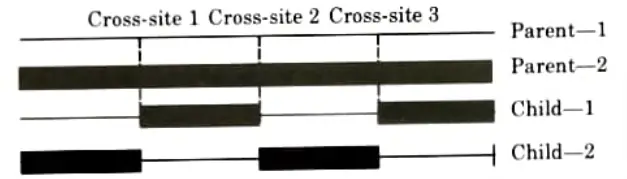
- vi. If the number of cross-sites is odd, then a different cross-point is always assumed at the string beginning. The information (genes) between alternate pairs is exchanged as shown in Fig.


4. Uniform Crossover:
- i. In a uniform crossover operator, each bit from either parent is selected with a probability of 0.5 and then interchanged as shown in Fig.(a).
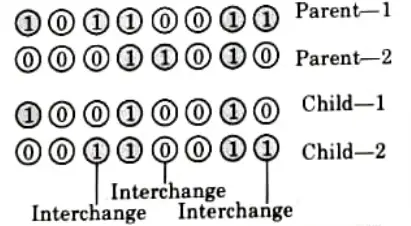




- ii. Uniform crossover is not the same as one-point crossover.
- iii. Genes in offspring are sometimes synthesized by copying the relevant gene from one or both parents using a randomly generated crossover mask.
- iv. When the mask is set to 1, the gene is copied from the first parent; when it is set to 0, the gene is copied from the second parent, as shown in Fig (b).
- v. The process is repeated, but this time the parents are switched to generate the second offspring.
- vi. offspring therefore contains a mixture of genes from each parent. The number of effective crossing points is not fixed but averages to L/2 (where L is chromosome length).
b. How is weight adjustment done in back propagation network ?
Ans.
- 1. The algorithm is used to effectively train neural networks using a technique known as chain rule.
- 2. In simple terms, back propagation performs a backward pass over a network after each forward pass while modifying the model’s parameters (weights and biases).
- 3. Back propagation attempts to optimise the cost function by modifying the weights and biases of the network.
- 4. The gradients of the cost function with respect to those parameters define the level of adjustment.
- 5. Gradient of a function C(x1,x2,…..xm) in point x is a vector of the partial derivatives of C in x.
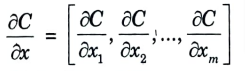
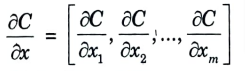
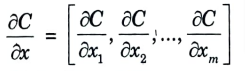
Equation for derivative of C in x.
- 6. A function’s derivative C assesses the function’s (output value’s) sensitivity to change in response to a change in its parameter (input value). In other words, the derivative indicates the direction of C. The gradient indicates how much the parameter x must be changed (in either a positive or negative direction) to minimise C.
- 7. To compute those gradients, we employ a technique known as chain rule.
- 8. Using this chain method, we shall compute the gradient of C in relation to a single weight.
c. What is defuzzification ? Explain all the three methods which are used in defuzzification with an example?
Ans. Defuzzification:
- 1. Defuzzification is the conversion of a fuzzy set to a crisp set.
- 2. It is a mapping from a fuzzy control action space defined over an output universe of discourse to a non-fuzzy (crisp) control action space. It’s most popular in fuzzy control systems.
- 3. They will include a collection of rules that will turn a set of variables into a fuzzy result, which will be defined in terms of membership in fuzzy sets.
- 4. Defuzzification is the process of converting the fuzzy set membership degrees into a definite choice or real value.
Different methods of defuzzification process are:
a. Center of Area (COA): The centroid defuzzification method selects the output crispy value corresponding to the center of gravity of the output membership function which is given by the expression:
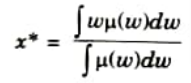
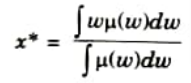
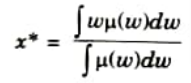
b. Center of Sums (COS):
1. This is the most commonly used defuzzification technique.
2. In this method, the overlapping area is counted twice.
3. COS builds the resultant membership function by taking the algebraic sum of outputs from each of the contributing fuzzy sets
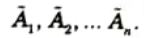
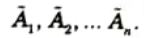
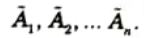
4. The defuzzified valued x* is defined as:
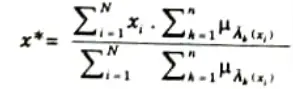
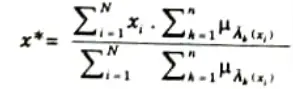
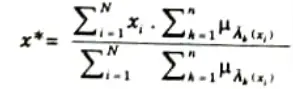
Here, n is the number of fuzzy sets, N is the number of fuzzy
variable, 𝝁𝝀(xi) is the membership function for the kth fuzzy set.
c. Height Method (HM):
i. In the height method, the centroid of output membership function for each rule is evaluated first.
ii. The final output is then calculated as the average of the individual centroids, weighted by their heights (degree of membership) as follows:
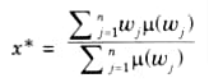
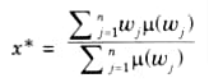
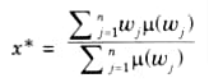
d. Middle of Maxima (MOM):
i. The MOM strategy generates a control action which represents the mean value of all local control actions whose membership functions reach the maximum and may be expressed as:
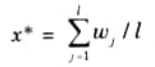
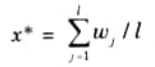
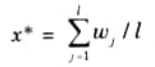
e. Center of Largest Area (COLA):
i. The COLA method is used in the case when universe of discourse WIs non-convex, i.e., it consists of at least two convex fuzzy subsets.
ii. Then the method determines the convex fuzzy subset with the largest area and defines the crisp output value x* to be the center of area of this particular fuzzy subset.
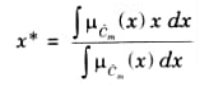
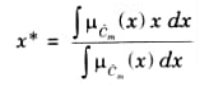
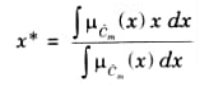
f. Height Weighted Second Maxima (HWSM):
i. In this method, the second maximum of each output membership function for each rule is evaluated first.
ii. The final output is calculated as the average of the individual maxima, weighted by their heights (degree of membership) as follows:
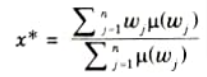
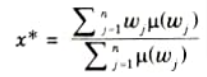
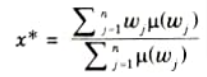
where wj takes the largest value of the domain with maximal membership degree.
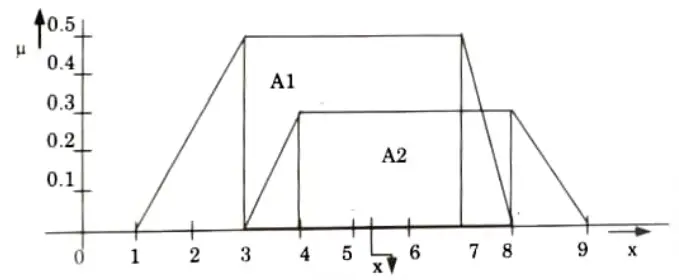
Example of defuzzification:
Center of sum (COS): The aggregated fuzzy set of two fuzzy sets C1 and C2 is shown in Fig. Let the area of this two fuzzy sets are A1 and A2.
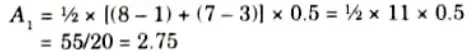
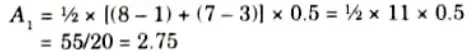
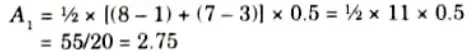
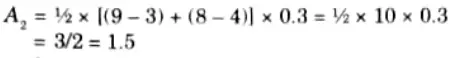
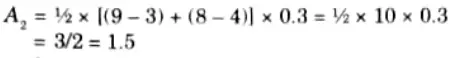
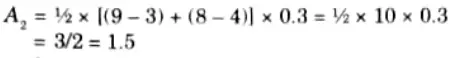
Now the center of area of the fuzzy set C1 is
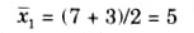
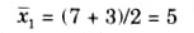
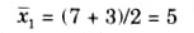
The center of area of the fuzzy set C2 is
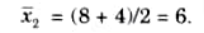
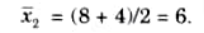
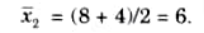
Now the defuzzified value
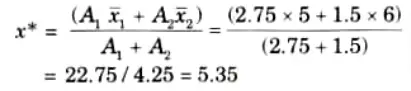
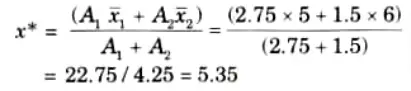
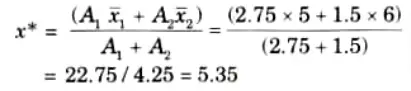


d. What is multilayer perceptron? How is different from single layer perceptron?
Ans. Multilayer perceptron:
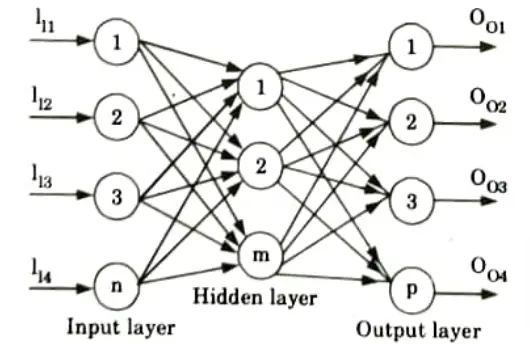
- 1. A multilayer perceptron is a feed forward artificial neural network class.
- 2. A multilayer perceptron model includes three layers: an input layer, an output layer, and a layer in between that is not directly connected to either the input or the output and is hence referred to as the hidden layer.
- 3. We utilise sigmoidal or squashed-S function for perceptrons in the input layer and linear transfer function for perceptrons in the hidden and output layers.
- 4. Because the input layer’s purpose is to distribute the values it receives to the next layer, it does not conduct a weighted sum or threshold.
- 5. The input-output mapping of multilayer perceptron is shown in Fig. and is represented by


- 6. Unless there is a non-linear activation function between layers, a multilayer perceptron does not boost computational capacity over a single layer neural network.
Difference:
| S. No. | Single layer perceptron model | Multilayer perceptron model |
| 1. | It does not contain any hidden layer. | It contains one or more hidden layer. |
| 2. | It can le arn only linear function. | It can learn linear and non-linear function. |
| 3. | It requires less training input. | It requires more number of training inputs. |
| 4. | Learning is faster. | Learning is slower. |
| 5. | Faster execution of the final network. | Slower execution of the final network. |
e. Discuss neuro fuzzy system and rule base structure identification in detail.
Ans. Neuro fuzzy system:
- 1. A neuro fuzzy system is a fuzzy system that processes data samples to determine its parameters (fuzzy sets and fuzzy rules) using a learning method developed from or influenced by neural network theory.
- 2. A neuro fuzzy system is based on a fuzzy system that has been taught using a neural network learning method. The (heuristical) learning technique operates on local input and results in only local changes to the underlying fuzzy system.
- 3. The Neuro fuzzy system includes the human-like reasoning style of fuzzy systems by utilizing fuzzy sets and a language model comprised of a collection of IF-THEN fuzzy rules.
- 4. A neuro fuzzy system is a three-layer feed forward neural network. The first layer represents input variables, the middle (hidden) layer fuzzy rules, and the third layer output variables.
Rule base structure identification:
- 1. Fuzzy rule-base modeling is the challenge of defining the structure and parameters of a fuzzy F-THEN rule base in order to accomplish the required input/output mapping.
- 2. System modeling is closely related to interpolative input-output mapping, pattern categorization, case-based reasoning, and example-based learning.
- 3. It is crucial in rule-based control, data compression, pattern recognition, expert systems, and multi-objective decision making.
- 4. A fuzzy inference system describes a system using fuzzy IF-THEN principles.
Fuzzy IF-THEN rules:
1 Fuzzy rules take the form:
IF(conditions) and THEN (actions)
where conditions and actions are linguistic variables, respectively.
2. These rules encode the knowledge about a system.
3. If THEN rule in the form of fuzzy set is given as
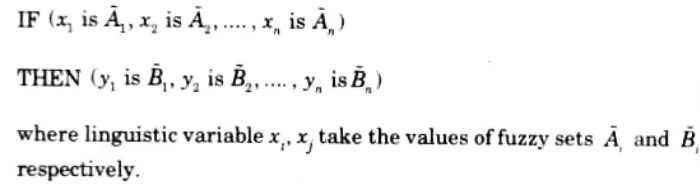
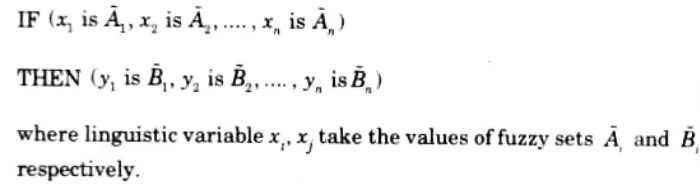
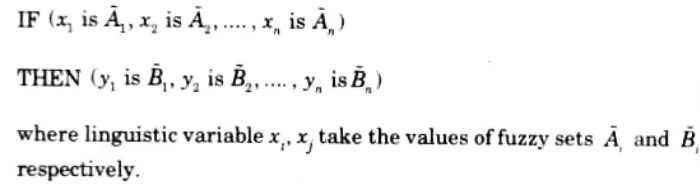
For example: IF temperature is very cold THEN air conditioner is off.
Section 3: Supervised and Unsupervised Learning
a. How back propagation network works in ANN ? Write an algorithm for it.
Ans. Back propagation learning algorithm: Step 1: Normalize the inputs and outputs with respect to their maximum values. For each
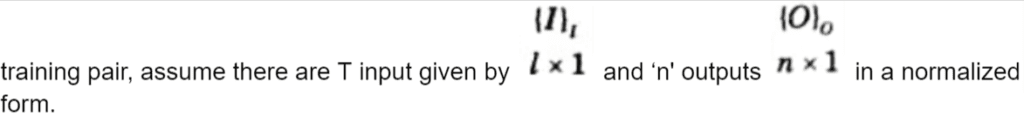
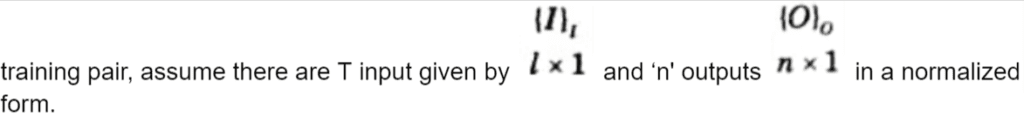
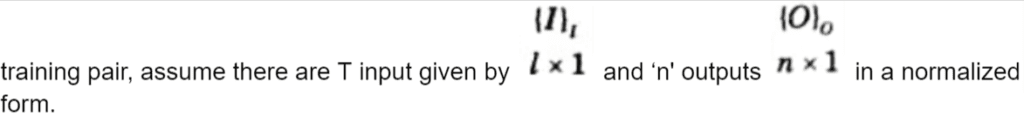
Step 2: Assume the number of neurons in the hidden layer lies between l < m < 2l.
Step 3: [V] Represents the weight of synapses connecting input neurons and hidden neurons and [W] represents weights of synapses connecting hidden neurons and output neurons. Initialize the weights to small random values from – 1 to 1. For general problems, 𝝀 can be assumed as 1 and the threshold values can be taken as zero.



Step 4: For the training data, present one set of inputs and outputs by using linear activation function as :



Step 5: Compute the inputs to the hidden layer by multiplying corresponding weights of synapses as:



Step 6: Let the hidden layer units evaluate the output using the sigmoidal function as:
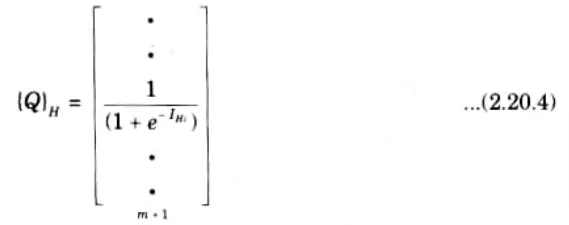


Step 7: Compute the inputs to the output layer by multiplying corresponding weights of synapses as



Step 8: Let the output layer units evaluate the output using sigmoidal function as



Step 9: Calculate the error and the difference between the network output and the desired output as for the ith training set as



Step 10: Find {d} as
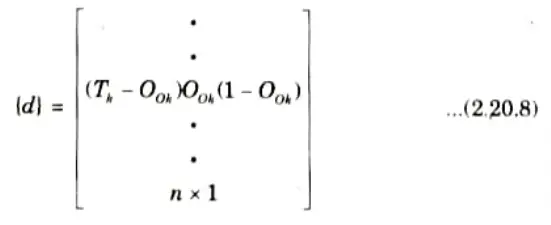
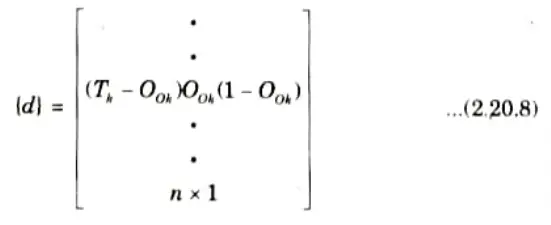
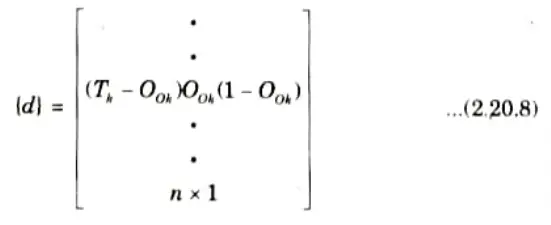
Step 11: Find [Y] matrix as



Step 12: Find
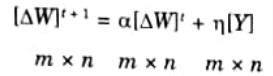
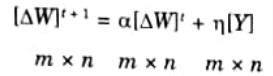
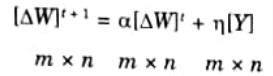
Step 13: Find
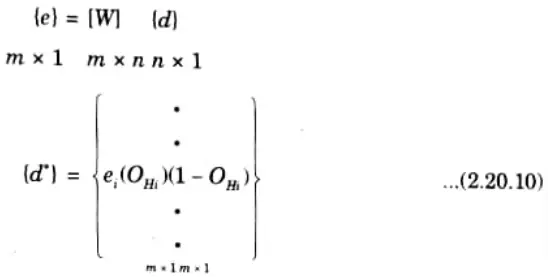
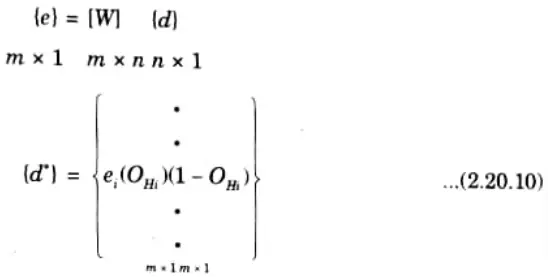
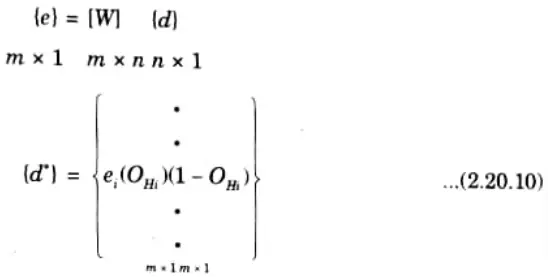
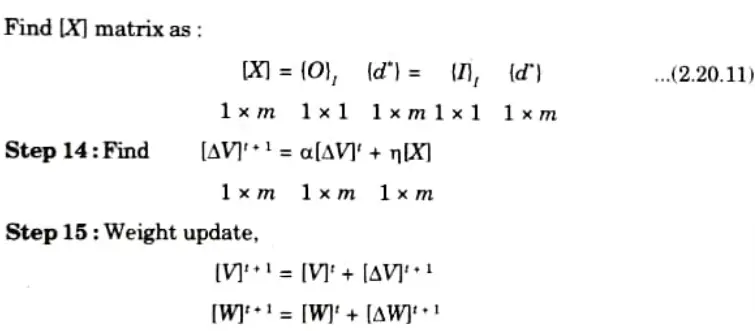
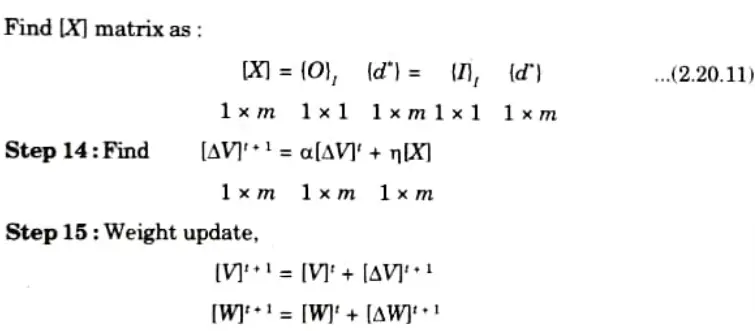
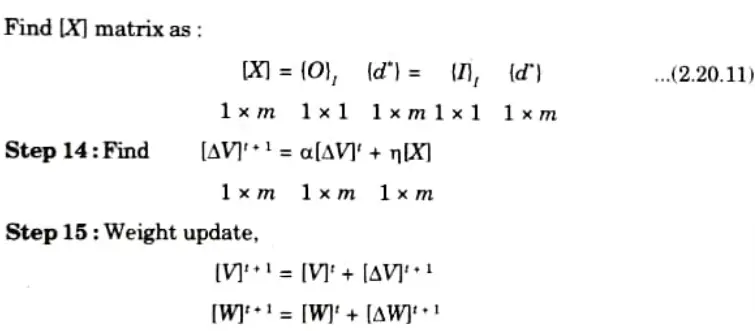
Step 16: Find error rate as
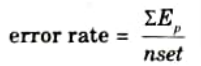
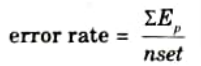
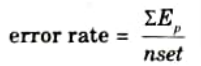
Step 17: Repeat steps 4-16 until the convergence in the error rate is less than the tolerance value.
b. Explain supervised and unsupervised learning in detail.
Ans. 1. Supervised learning:
- i. Learning is performed with the help of a trainer.
- ii. In ANN, each input vector requires a corresponding target vector, which represents the desired output.
- iii. The input vector along with target vector is called training pair.
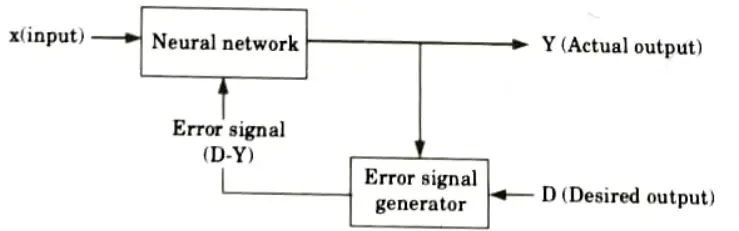


- iv. The input vector results in output vector.
- v. The actual output vector is compared with desired output vector.
- vi. If there is a difference means an error signal is generated by the network. It is used for adjustment of weights until actual output matches desired output.
2. Unsupervised learning:
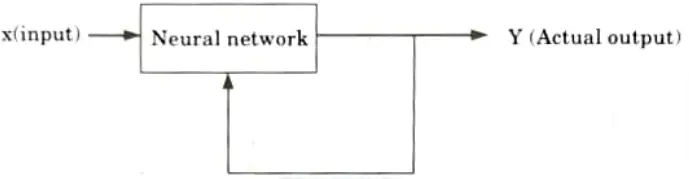


- i. Learning is done without the assistance of a trainer.
- ii. During the training process, the network accepts input patterns and arranges them into clusters. There is no feedback from the environment to inform what the output should be or whether it is correct.
- iii. The network discovers patterns, regularities, features/categories, and relationships for the input data over the output.
- iv. Precise clusters are generated by recognising similarities and differences, a process known as self-organization.
Sector 4: Feedback Control System
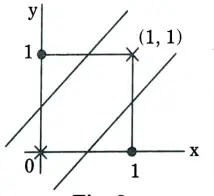
a. Why perceptron is not able to handle the tasks which are not linearly separable ? Justify your answer using XOR Problem.
Ans.
- 1. A perceptron can only converge on linearly separable data. Therefore, it is not capable of imitating the XOR function.
- 2. A single-layer perceptron cannot implement XOR. The reason is because the classes in XOR are not linearly separable.
- 3. We cannot draw a straight line to separate the points (0, 0), (1, 1) from the points (0, 1), (1, 0).
- 4. There is no single function that produces a hyperplane capable of separating the points of the XOR function. The curve in the image separates the points, but it is not a function.
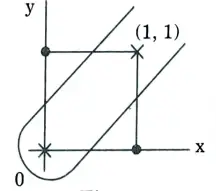


5. To separate the points of XOR, we have to use at least two lines (or any other shaped functions). This will require two separate perceptrons.


b. Write a short note on the following:
i. Feedback control system
ii. Fuzzy automata
Ans. i. Feedback control system:
- 1. A feedback control system is essentially a control system whose output is determined by the generated feedback signal.
- 2. The feedback control system is in charge of processing feedback signals, which serve as input to the system.
- 3. A feedback control system is made up of many components such as resistors, transistors, and other electrical appliances that perform basic functions.
- 4. The comments can be further classified as either favourable or negative.
ii. Fuzzy automata:
- 1. Fuzzy automata are employed to deal with system uncertainty because classical automata are incapable of dealing with system uncertainty.
- 2. A fuzzy automata is a broader form of a non-deterministic finite automaton.
- 3. Fuzzy automata can be utilised in a variety of applications, including neural networks, artificial intelligence, learning systems, controlling systems, databases, system modelling, pattern matching, searching, script recognition, databases, lexical analysis, string matching, and many others.
- 4. Membership values are important in fuzzy automata. We can compute the membership values using various lattices, including lattice-ordered monoid, complete lattice, complete residuated lattice, and other algebraic structures.
- 5. To determine the fuzzy language in fuzzy automata, we can utilise compositional approaches such as minmax automaton, max-min automaton, and max-product automaton.
- 6. In classical automata theory, strings are either accepted or rejected, whereas in fuzzy automata theory, strings are accepted with a specific membership value.
Section 5: Fuzzy Inference System
a. Explain the architecture of Kohnen self organizing network.
Ans.
- 1. Kohnen the model captures the essential features of computational maps in the brain and yet remains computational tractable.
- 2. It appears that the Kohonen model is more general than Willshaw Von Der Malsburg model in the sense that it is capable of performing data compression i.e., dimensionality reduction on the input.
- 3. The Kohonen model belongs to the class of vector coding algorithm.
- 4. The model provides a topological mapping that optimally places a fixed number of vectors i.e., code words into higher dimensional input space and thereby facilitates data compression.
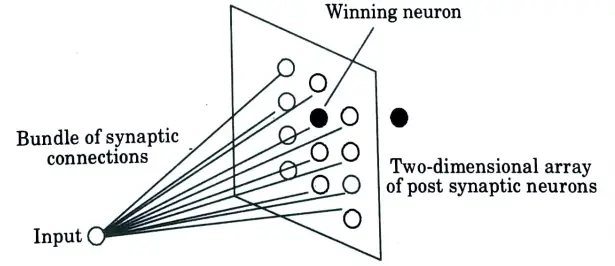


Therefore Kohonen model derived in two ways:
- 1. Self organization: Self organization motivated by neurobiological consideration, to derive the model.
- 2. Vector quantization: In this approach that uses a model involving an encoder and decoder.
b. Explain fuzzy inference system with all its components in detail.
Ans. Fuzzy inference system:
- 1 Inferences is a technique where facts, premises F1,F2,…….., Fn and a goal G is to be derived from a given set.
- 2. Fuzzy inference is the process of formulating the mapping from a given input to an output using fuzzy logic.
- 3. The mapping then provides a basis from which decisions can be made.
- 4. Fuzzy inference (approximate reasoning) refers to computational procedures used for evaluating linguistic (IP-THEN) descriptions.
- 5. The two important inferring procedures are:
- a. Generalized Modus Ponens (GMP).
- b. Generalized Modus Tollens (GMT).
Components:
i. Generalized Modus Ponens (GMP):
1. GMP is formally stated as
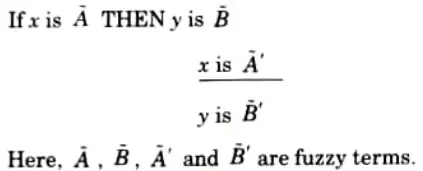
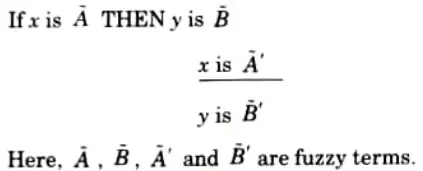
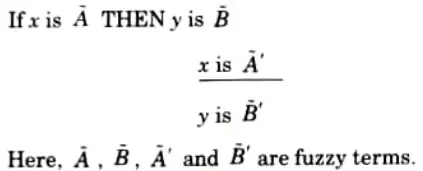
2. Every fuzzy linguistic statement above the line is analytically known and what is below is analytically unknown.
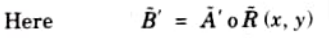
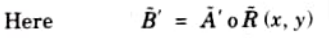
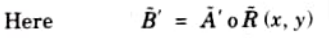
where ‘o’ denotes max-min composition (IF-THEN relation)
3. The membership function is



ii. Generalized Modus Tollens (GMT)
1. GMT is defined as
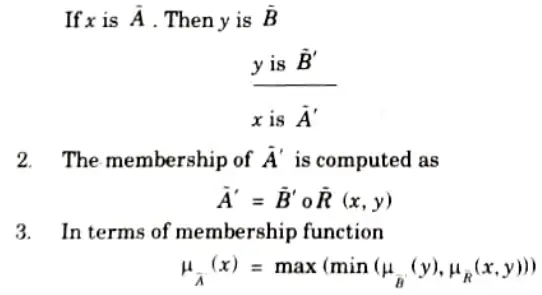
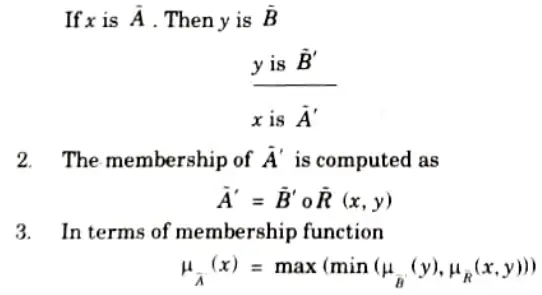
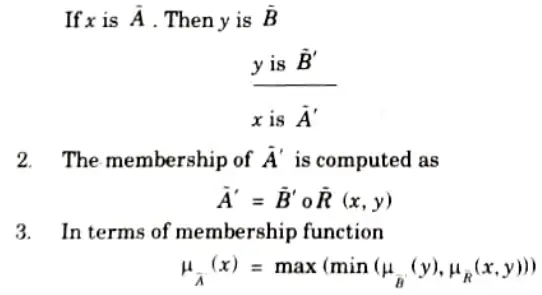
Section 6: Genetic Algorithm in Application of Soft Computing
a. How can fitness functions be found for any optimization problem ? Maximize the function f(x) = x2, with x in the integer interval (0, 31) with the help of Genetic Algorithm.
Ans.
- 1. The fitness function simply defined is a function which takes a candidate solution to the problem as input and produces as output how “fit” our how “good” the solution is with respect to the problem in consideration.
- 2. Calculation of fitness value is done repeatedly in a GA and therefore it should be sufficiently fast. A slow computation of the fitness value can adversely affect a GA and make it exceptionally slow.
- 3. A fitness function should possess the following characteristics:
- a. The fitness function should be sufficiently fast to compute.
- b. It must quantitatively measure how fit a given solution is or how fit individuals can be produced from the given solution.
Numerical:Step 1: For using genetic algorithms approach, one must first code the decision variable ‘x’ into a finite length string. Using a five bit (binary integer) unsigned integer, numbers between 0(00000) and 31(11111) can be obtained. The objective function here is f(x) = x2 which is to be maximized. Select initial population at random. Here initial population of size 4 is chosen, but any number of populations can be elected based on the requirement and application. Table show an initial population randomly selected.
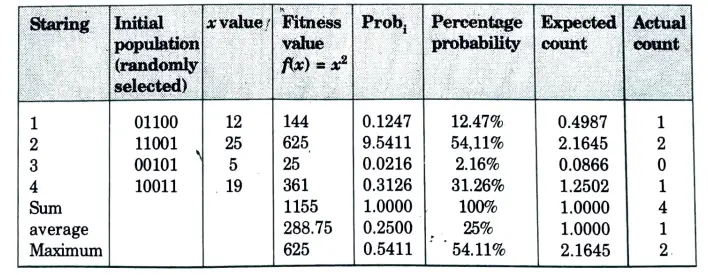


Step 2: Obtain the decoded x values for the initial population generated. Consider string 1, thus for all the four strings the decoded values are obtained.
Step 3: Calculate the fitness or objective function. This is obtained by simply squaring the ‘x’ value, since the given function isf(x) = x2. When, x = 12, the fitness value is, f(x) = 144 for x = 25, f(x) = 625 and so on, until the entire population is computed.
so on, until the entire population is computed.
Step 4: Compute the probability of selection,



𝚺f(x): Summation of all the fitness value of the entire population. Considering string 1, Fitness f(x) = 144, 𝚺f(x) = 1155.
The probability that string 1 occurs is given by, P1 = 144/1155 = 0.1247. The percentage probability is obtained as, 0.1247/100 = 12.47%.
The same operation is done for all the strings. It should be noted that, summation of probability select is 1.
Step 5: The next step is to calculate the expected count, which is calculated as,
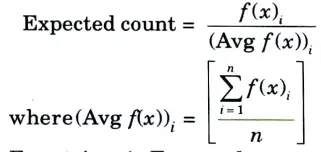
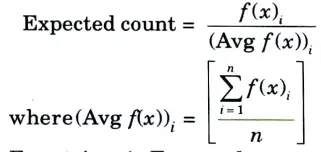
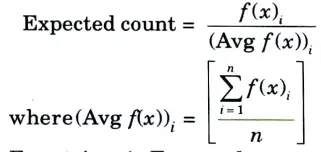
For string 1, Expected count = Fitness/Average = 144/288.75 = 0.4987.
Computing the expected count for the entire population. The expected count gives an idea of which population can be selected for further processing in the mating pool.
Step 6: Now, as stated in Table, write the mating pool depending on the actual count. Because the actual count of string no 1 is one, it appears just once in the mating pool. Because string no 2 has a count of two, it appears twice in the mating pool. Because the actual count of string number three is zero, it does not appear in the mating pool. Similarly, the actual count of string no 4 is 1, indicating that it occurs only once in the mating pool. The mating pool is generated as a result of this.
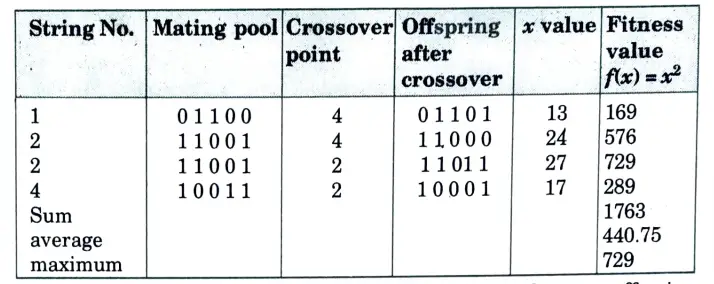


Step 7: Crossover operation is performed to produce new offspring (children). The crossover point is specified and based on the crossover point, single point crossover is performed and new offspring is produced. The parents are:
Parent1: 1 0 1 1 0 0, Parent2: 2 1 1 0 0 1.
The offspring is produced as, Offspring 1 : 1 0 1 1 0 1 0 Offspring2: 2 1 1 0 0 0
In a similar manner, crossover is performed for the next strings.
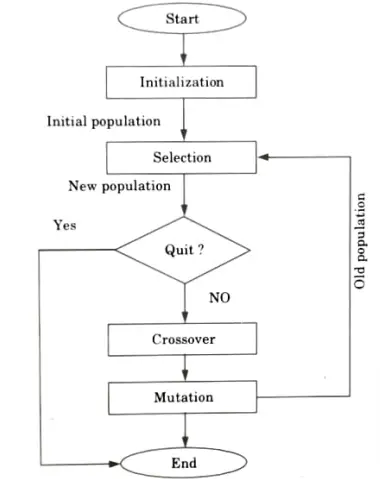
b. What is genetic algorithm ? Discuss the working of genetic algorithm with the help of flowchart.
Ans. Genetic algorithm (GA):
- 1. The genetic algorithm is a natural selection-based method for solving limited and unconstrained optimisation problems.
- 2. The genetic algorithm iteratively alters a population of individual solutions.
- 3. At each stage, the genetic algorithm chooses individuals at random from the present population to be parents and uses them to produce children for the following generation.
- 4. The population advances towards an optimal solution through subsequent generations.
Flow chart: The genetic algorithm uses three main types of rules at each step to create the next generation from the current population :
- a. Selection rule: Selection criteria determine which individuals, known as parents, contribute to the population in the next generation.
- b. Crossover rule: Crossover rules combine two parents to form children for the next generation.
- c. Mutation rule: Mutation rules apply random changes to individual parents to form children.


Section 7: Fuzzy and Crisp Relations in Application of Soft Computing
a. What are fuzzy sets? Discuss the various properties of fuzzy sets ?
Ans. Fuzzy sets:
1. Fuzzy set is a set having degree of membership between 1 and 0.
2. Fuzzy sets A(bar) in the universe of discourse U can be defined as set of ordered pair and it is given by
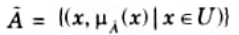
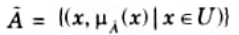
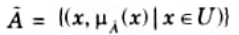
Where 𝛍A is the degree of membership of x in A(bar).
Properties of fuzzy sets: Let fuzzy set A(bar) is a subset of the reference set X. Also, the membership of any element belonging to the null set 𝝓 is 0 and the membership of any element belonging to the reference set is 1. Following are the properties:
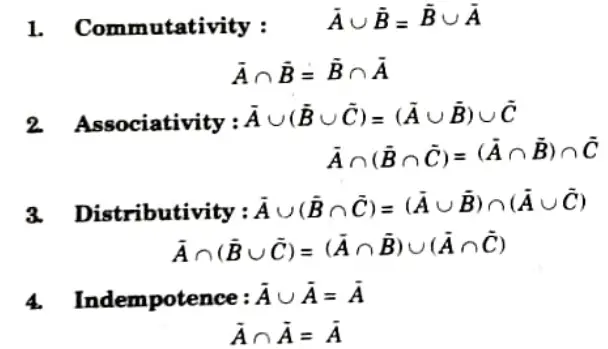
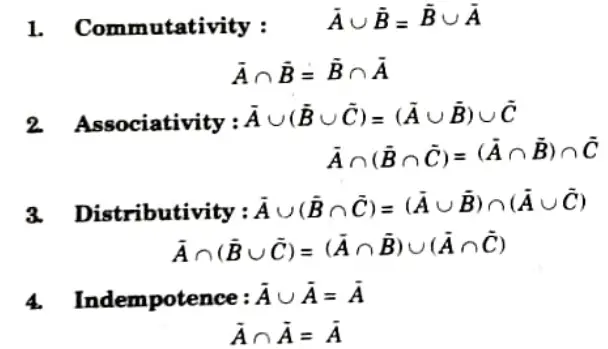
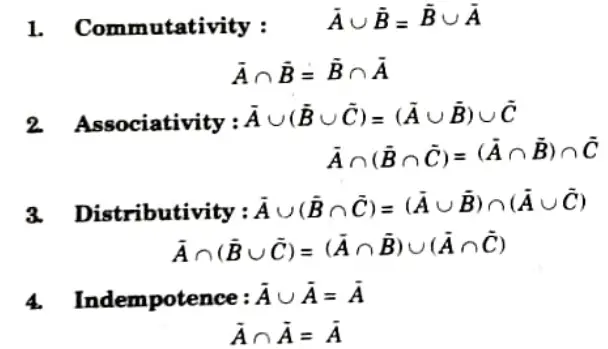



b. Write short note on the following:
i. Fuzzy Controllers
ii. Fuzzy and Crisp relations
Ans. i. Fuzzy controller:
- 1. A Fuzzy Logic Controller (FLC) a rule based system incorporating the flexibility of human decision making is used for fuzzy structural optimization.
- 2. The fuzzy functions are intended to represent a human expert’s conception of the linguistic terms.
Components of Fuzzy Logic Controller (FLC):
Fuzzy logic controller process is divided into three stages as shown in Fig.
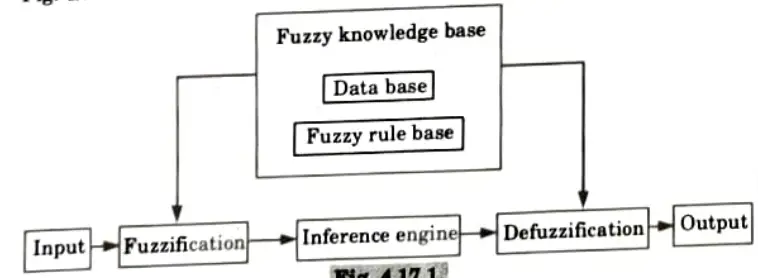


- a. Fuzzincation: It is a process evaluating the input variable with respect to corresponding linguistic terms in the condition side.
- b. Fuzzy inference: It is a process evaluating the activation strength of every rule base and combine their action sides.
- c. Defuzzification: It is process of converting the fuzzy output into precise numerical value.
ii. Fuzzy relations:
- 1. Fuzzy relation is a fuzzy set defined on the Cartesian product of crisp sets X1, X2,…….,Xn where the n-tuples (x1, x2,………,xn) may have varying degrees of membership within the relation.
- 2. The membership values indicate the strength of the relation between the tuples.
Crisp relations:
- 1. Crisp relation is defined over the cartesian product of two crisp sets. Suppose, A and B are two crisp sets. Then cartesian product denoted as A x B is a collection of order pairs, such that
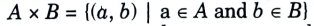
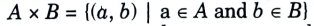
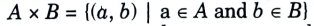
- 2. A crisp relation represents the presence or absence of association, interaction, or interconnectedness between the elements of two or more sets.
- 3. Crisp relation is set of order pairs (a, b) from cartesian product A x B such that a 𝞊 A and b 𝞊 B.
- 4. Relations basically répresent the mapping of the sets. It defines the interaction or association of variables.
- 5. The strength of the relationship between ordered pairs of elements in each universe is measured by the characteristic function denoted by 𝜘, where a value of unity is associated with complete relationship and a value of zero is associated with no relationship.

6 thoughts on “Application of Soft Computing Solved Question paper , Aktu Quantum”