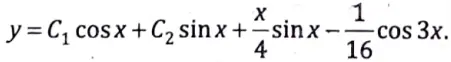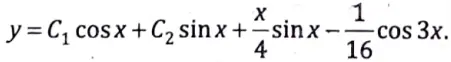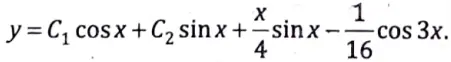Mathematics-III BCA Question Paper with Solutions, Book Pdf

Learn more about the Mathematics-III solved question paper for the BCA. Improve your mathematics skills with advanced calculus and numerical techniques while gaining insightful knowledge that will help you succeed in school.

Dudes 🤔.. You want more useful details regarding this subject. Please keep in mind this as well.

Important Questions For Mathematics-III:
* Important Short Questions
* Solved Question Paper
* Syllabus

Section A: Mathematics-III Very Short Question Solutions

Q1. Show that 

|z₁ + z₂|² + |z₁ – z₂|² = 2|z₁|² + 2|z₂|²

Ans. We have, 

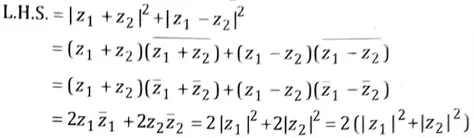
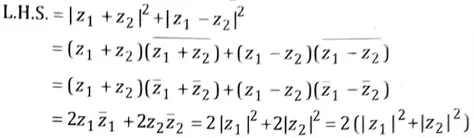
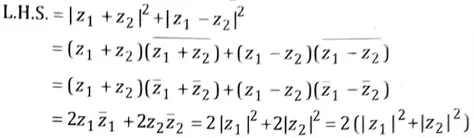
Q2. Define sequence with example. 

Ans. Let S be any non-empty set. A function whose domain is the set of N natural numbers and whose range is a subset of S, is called a sequence in the set S. 

Q3. If f(x, y, z) 3x²y – y³z² then find grad fat point (1, -2, -1). 

Sol. The gradient is a vector:  

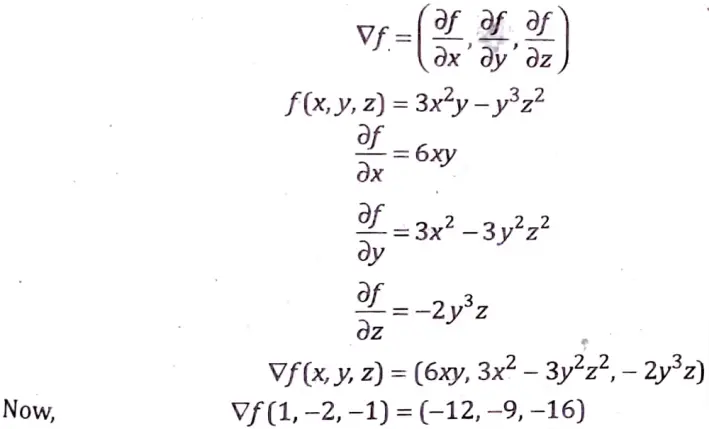
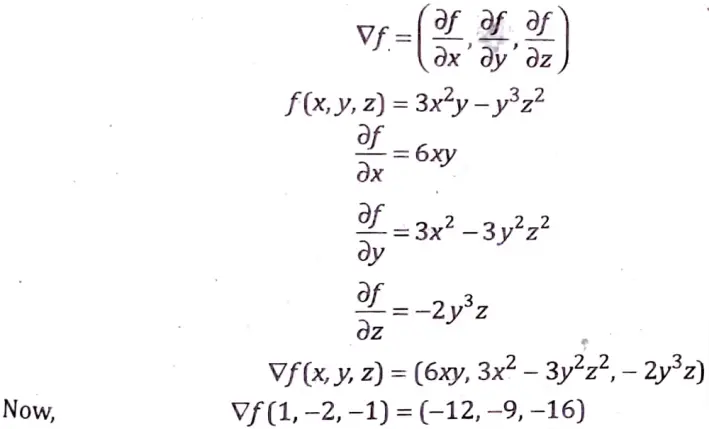
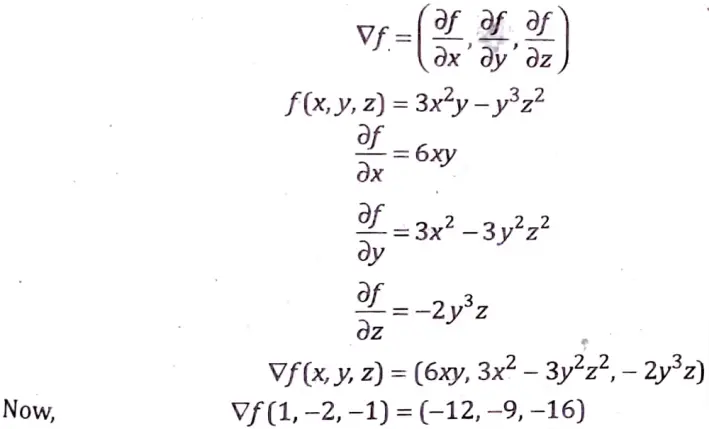
Q4. Solve

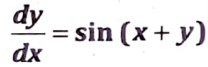
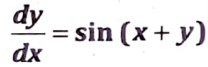
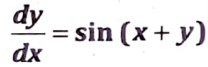
Sol. Let    x + y = z

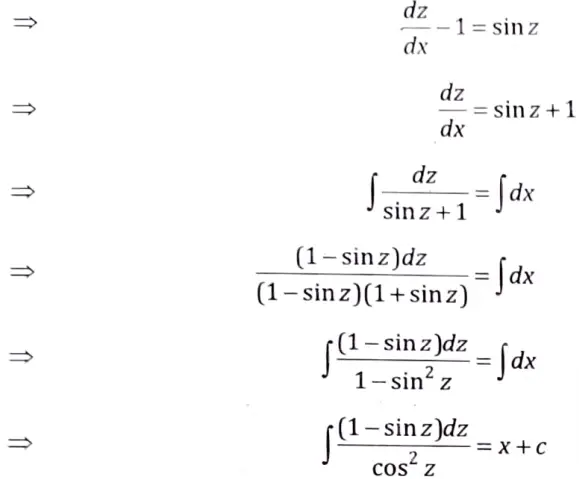
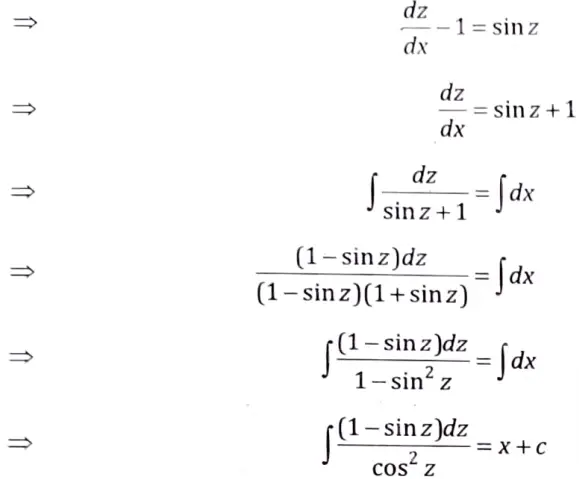
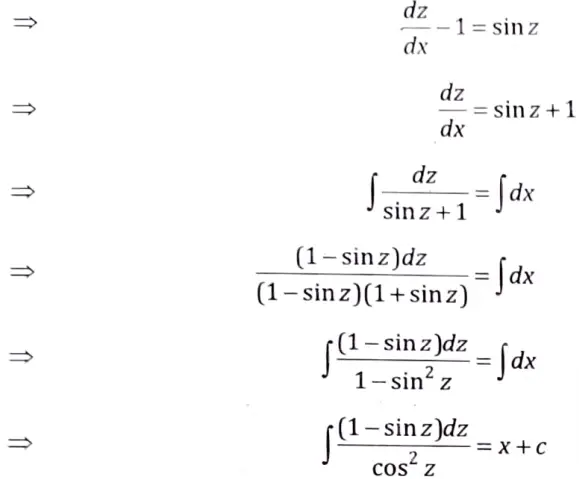
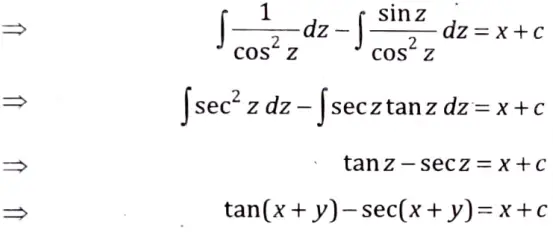
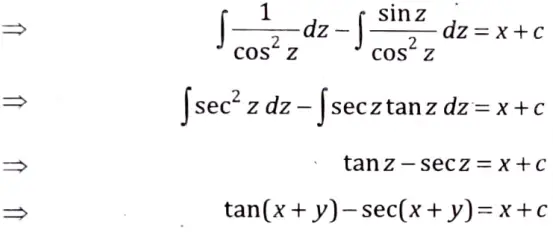
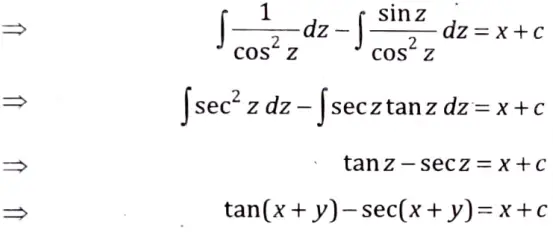
Q5. Solve

(D³ + 3D² + 3D + 1)y = e^x + e^-x 

Sol. Given equation is 

(D³ + 3D² + 3D + 1)y = e^x + e^-x 

∴ Auxillary equation is 

D³ + 3D² + 3D + 1 = 0 

∴ (D+ 1)³ =0  

∴ D = -1, -1, -1 are the roots. 

∴ C.F. = (c₁x² + c₂x + c₃) (e^x + e^-x) 

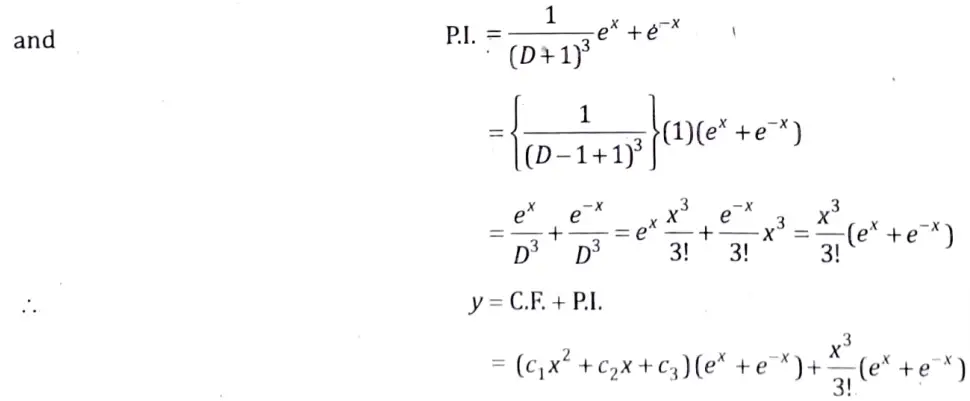
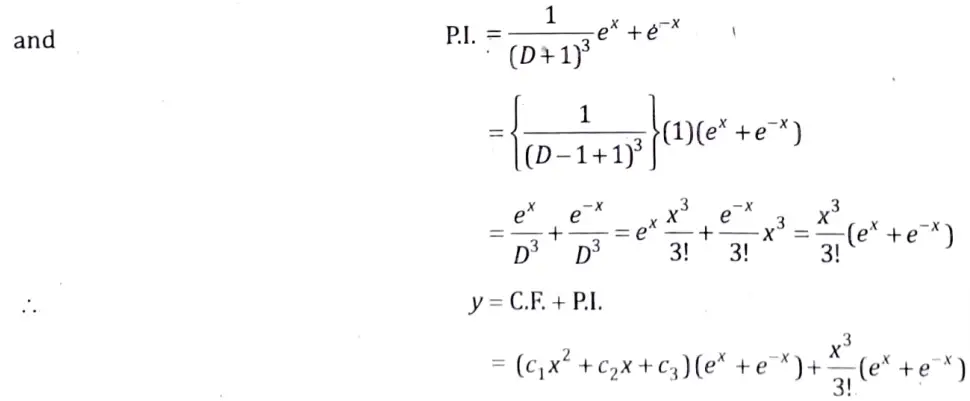
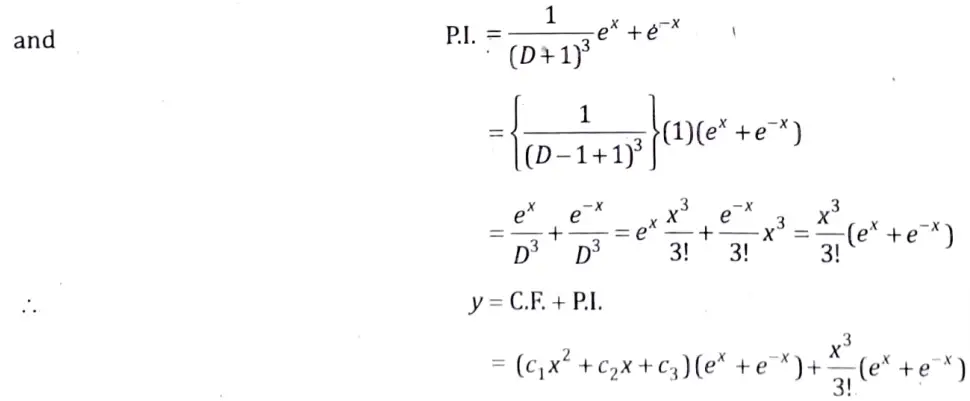
Section B: Mathematics-III Short Question Solutions

Q6. Determine the regions defined by 

|z-1| + |z + 1| ≤ 4  

Sol. Here, |z₁ -z₂| = |1 – (-1)| = 2 

and a = 4 

∴ |z₁ – z₂| < a

Since |z – z₀| + |z – z₁| = c (constant) is the equation of ellipse with z₀ and z₁ as focii, so |z – 1| + |z + 1| ≤ 4 is the equation of all points lying inside and on an ellipse with focii (1, 0) and (-1,0). 

Hence, region represented by |z – 1| + |z + 1| ≤ 4 is an interior and boundary of an ellipse. 

Q7. Solve

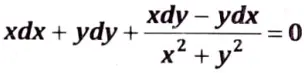
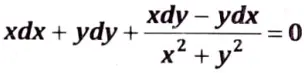
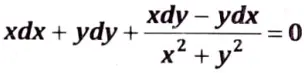
Ans. The given equation can be written as  

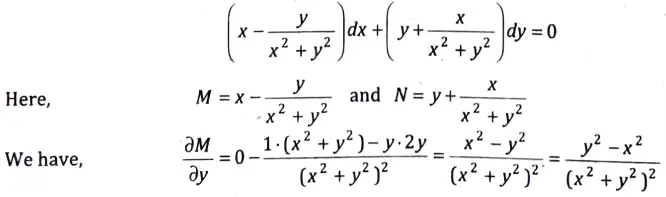
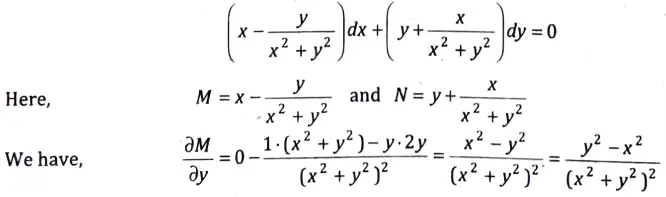
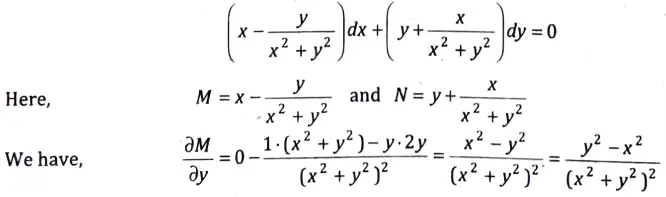
Q8. Show 

Sol. Given, 

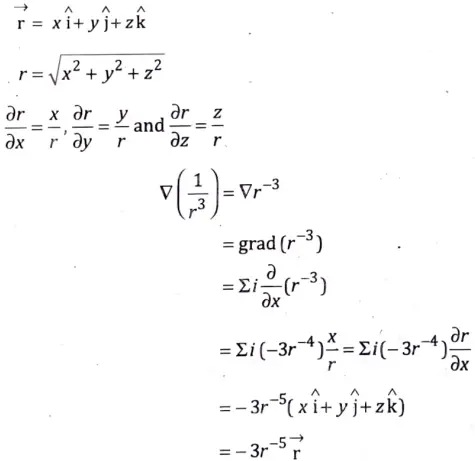
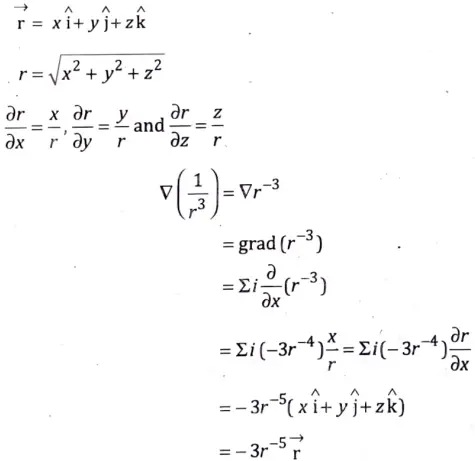
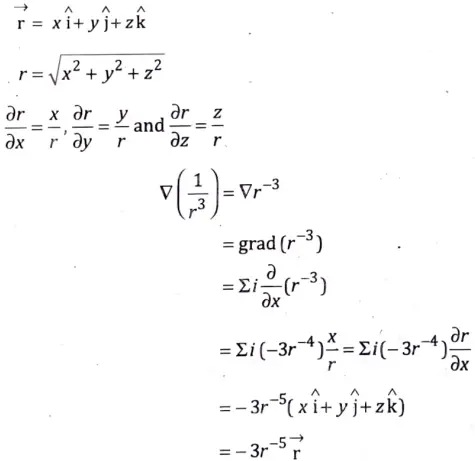
Section C: Mathematics-III Detailed Question Solutions

Q9. Show that

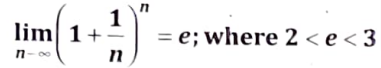
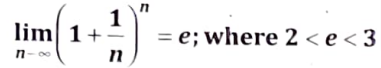
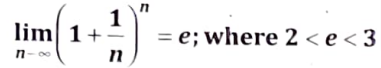
Sol. Let

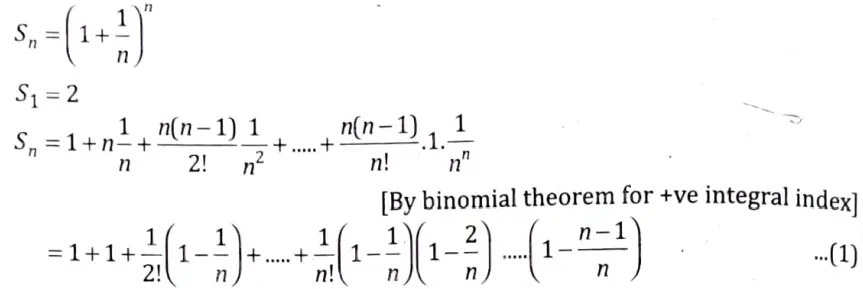
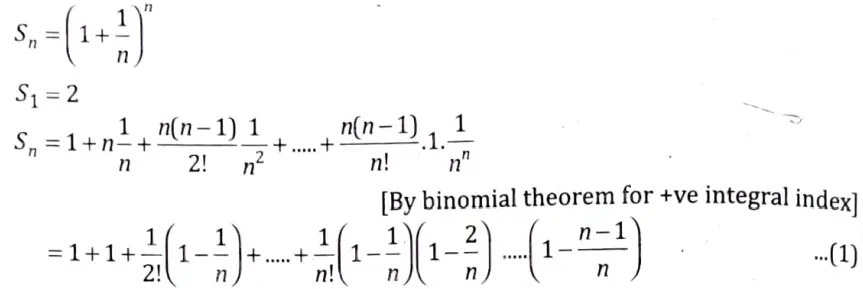
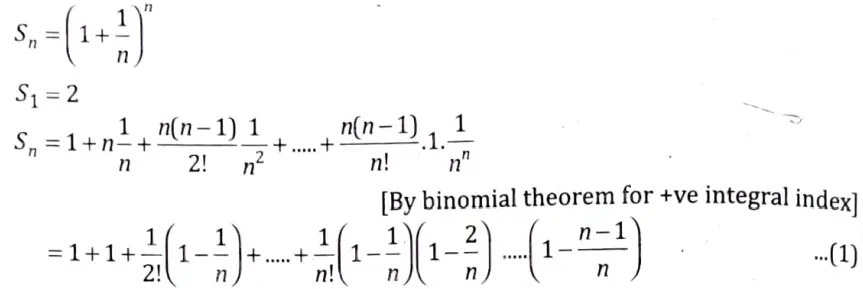
Similarly

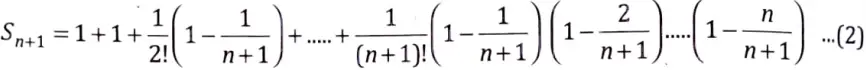
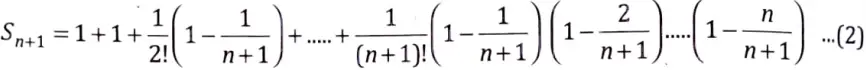
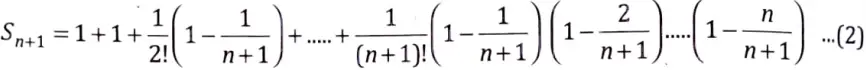
Comparing eqs. (1) and (2), we get 

S_n+1 ≥ S_n, ∀n

The sequence 〈S_n〉 is monotonically increasing. 

Now, from eq. (1), we have 

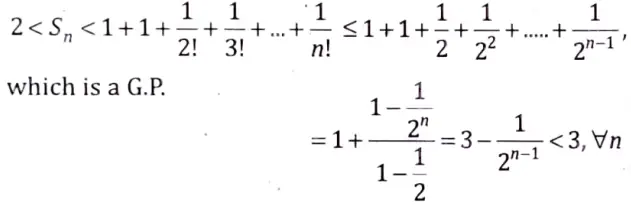
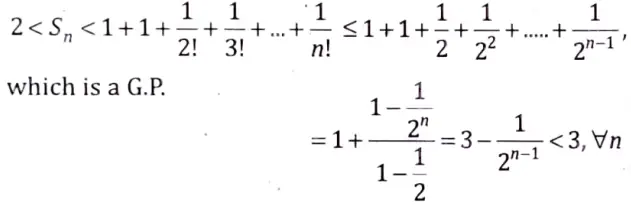
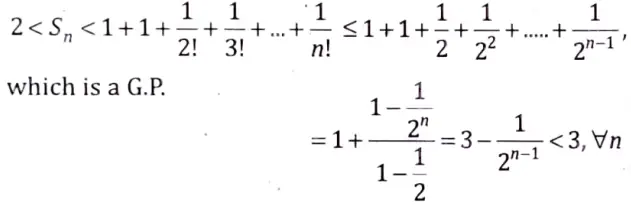
⇒ The sequence 〈S_n〉 is bounded.  

Thus, the sequence〈S_n〉, being a monotonically increasing sequence bounded above by 3 is convergent and equal to e where 2 < e < 3. 

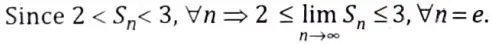
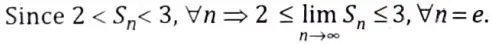
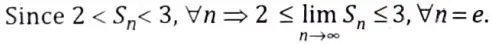
⇒ Limit of the sequence 〈S_n〉 lies between 2 and 3, i.e. = e.  

Q10. Test the convergence of following series. 

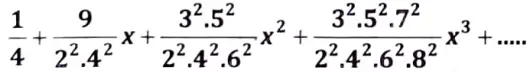
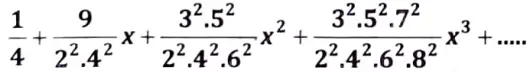
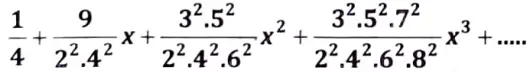
Sol. Here, we have  

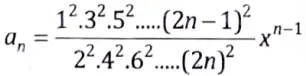
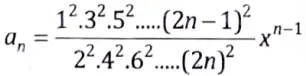
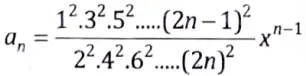
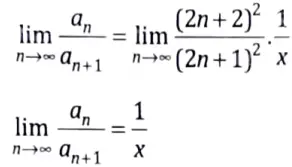
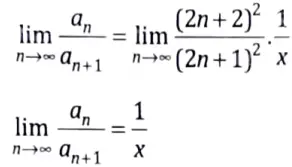
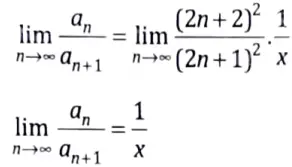
If x< 1,the series is convergent

If x > 1, the series is divergent 

If x = 1, 

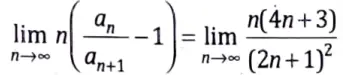
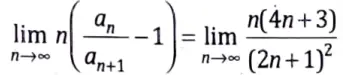
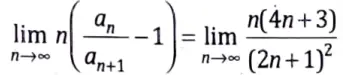
Therefore, we have to use another test. 

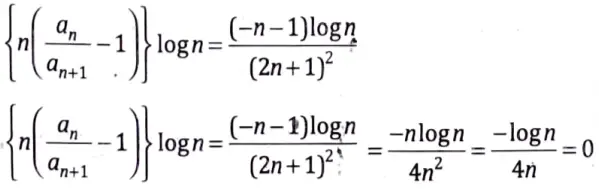
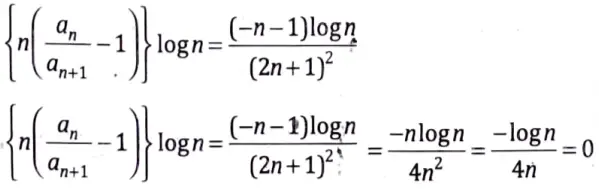
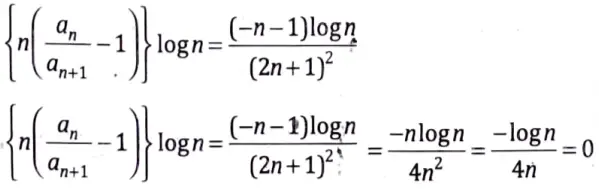
Hence, given series is divergent. 

Q11. Obtain the Fourier series of 

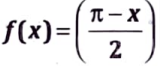
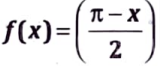
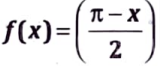
in the interval (0, 2𝝅) and hence deduce 

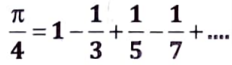
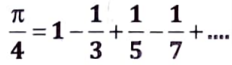
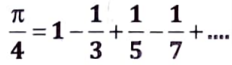
Sol. Fourier series off(x) having period 2𝝅, 0 

The formula of Fourier series is 

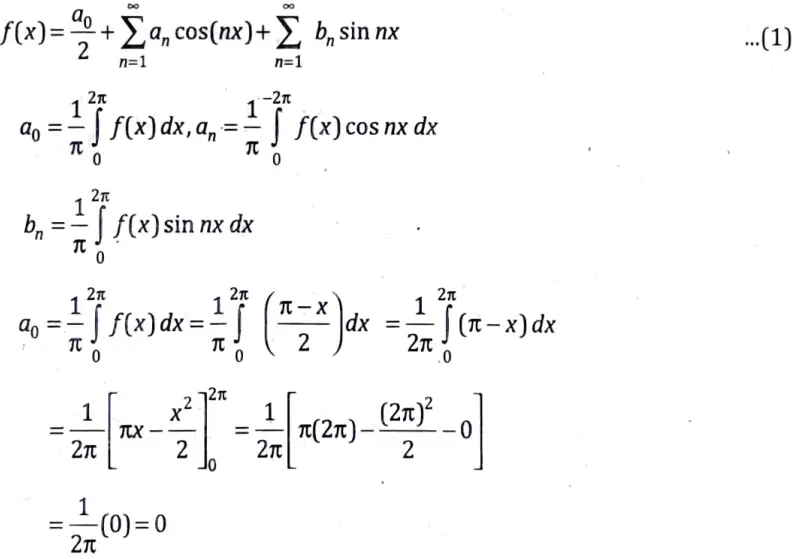
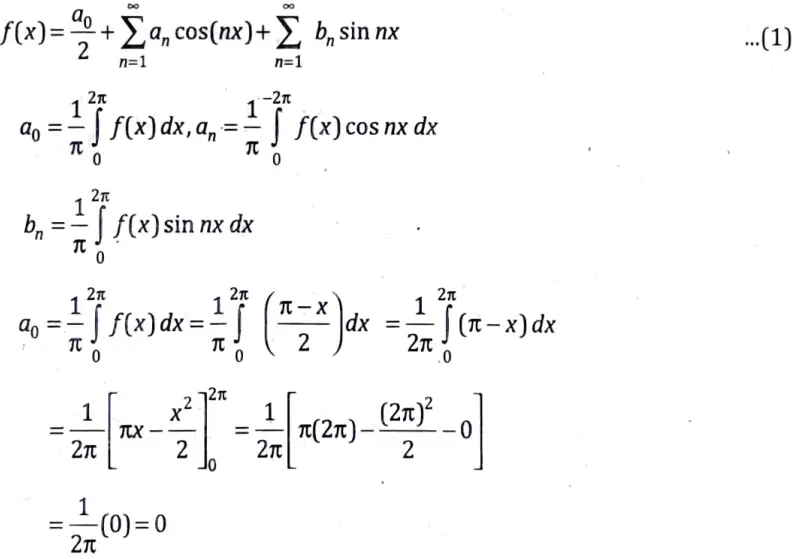
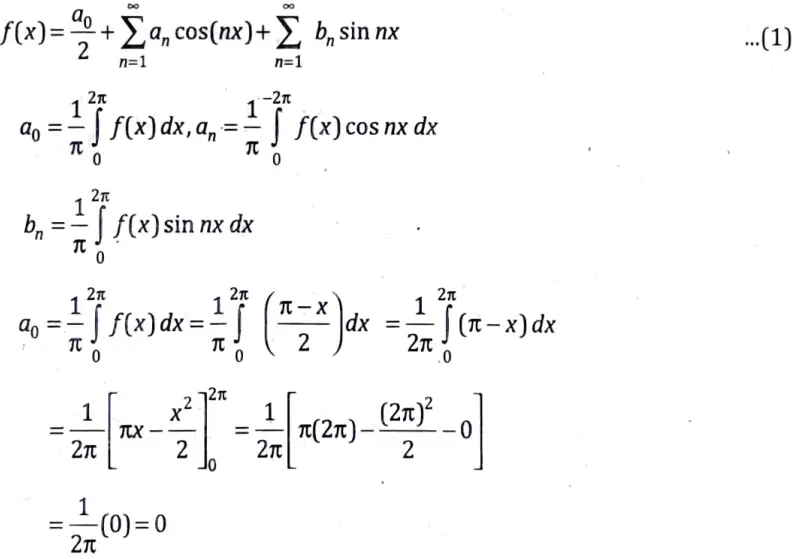
a₀ = 0 

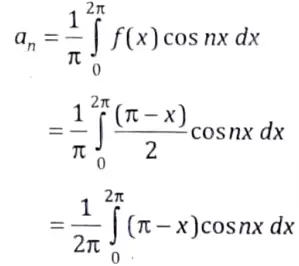
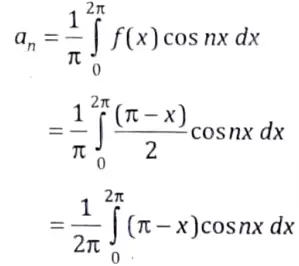
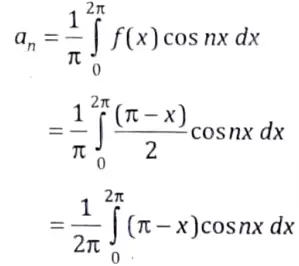
From Bernoulli rule

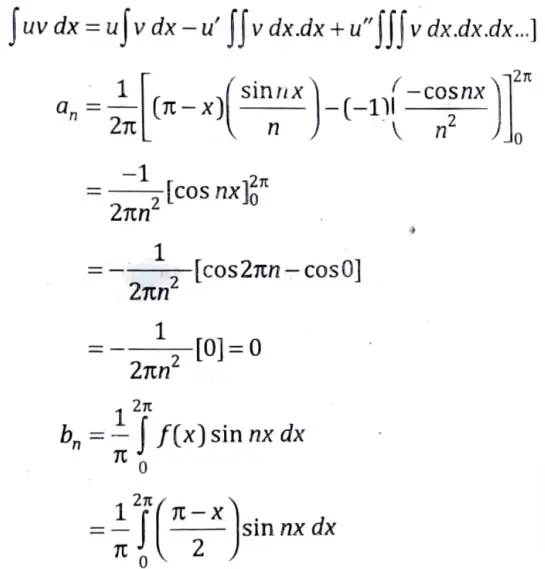
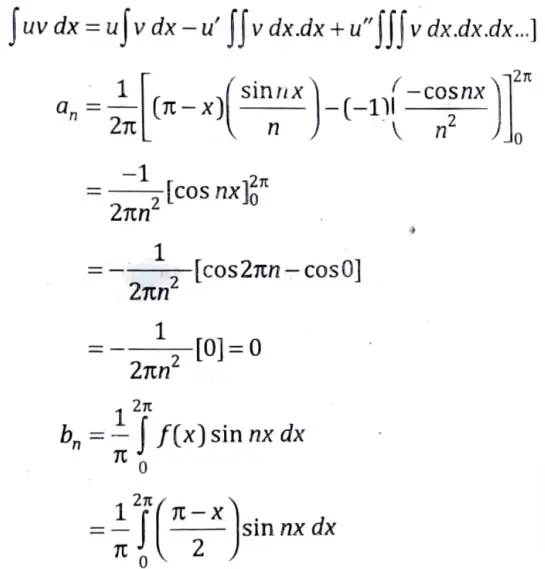
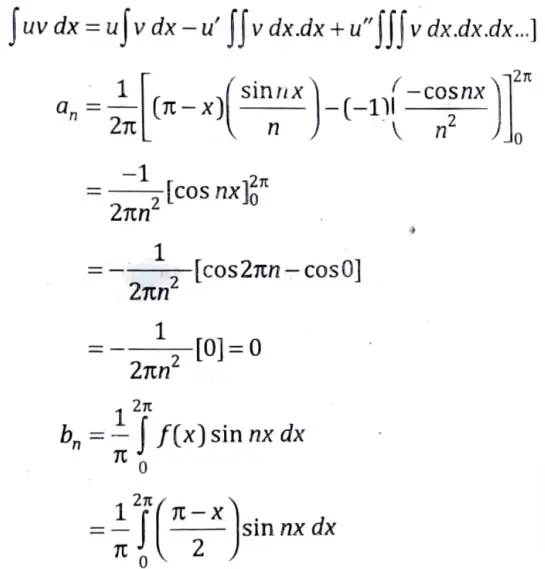
Apply Bernoulli rule  

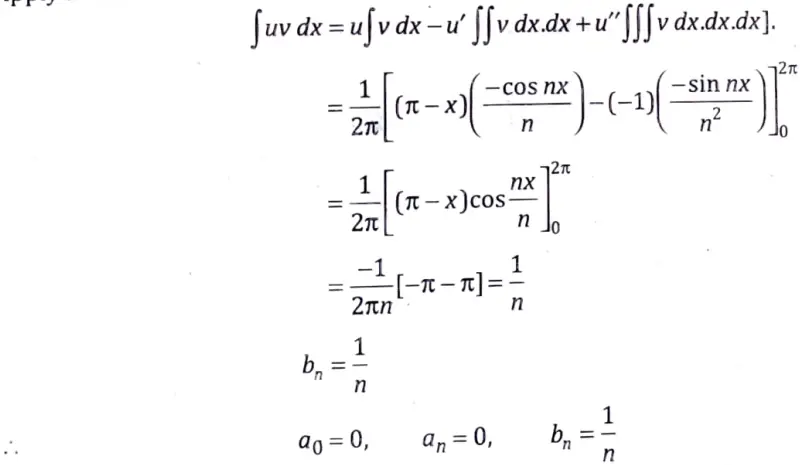
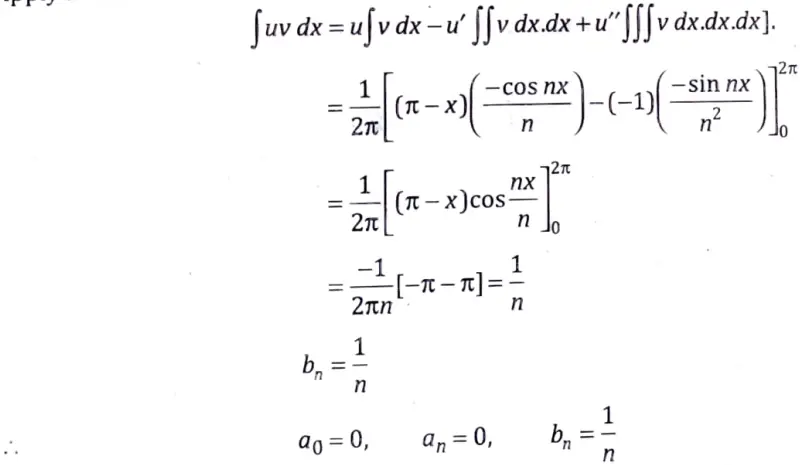
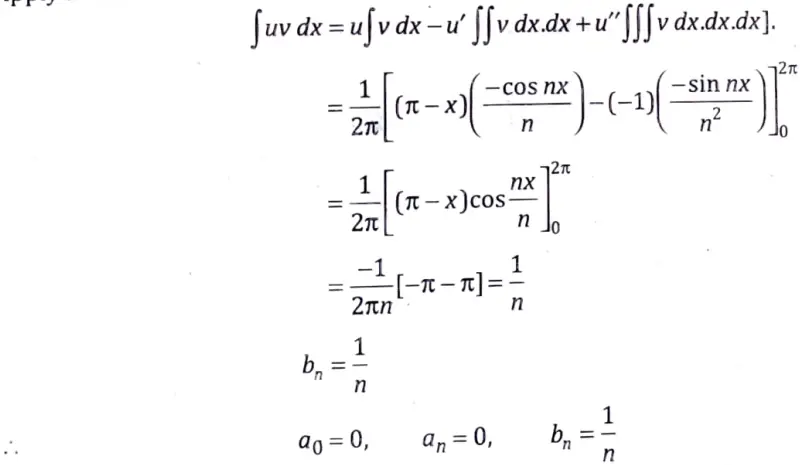
Substitute a₀, a_n, b_n in Fourier series, we get

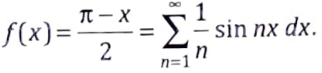
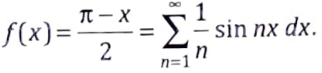
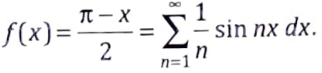
12. Solve

(1 +  y²)dx – (tan^-1y – x)dy = 0 

Sol. The given differential equation can be written as

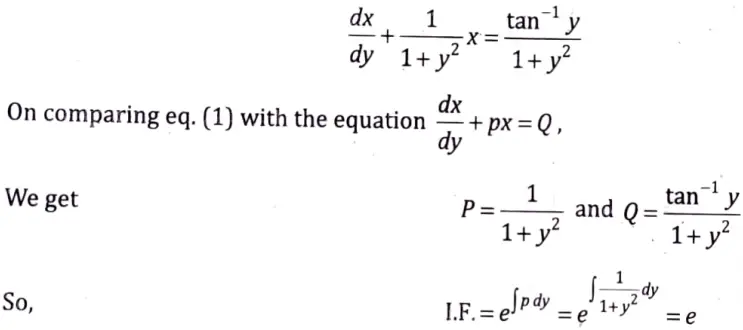
Thus, the solution of eq. (1) is  

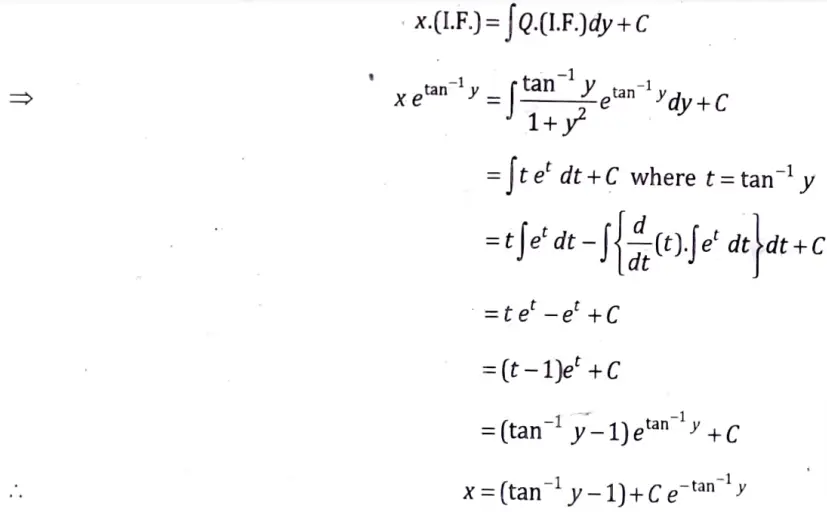
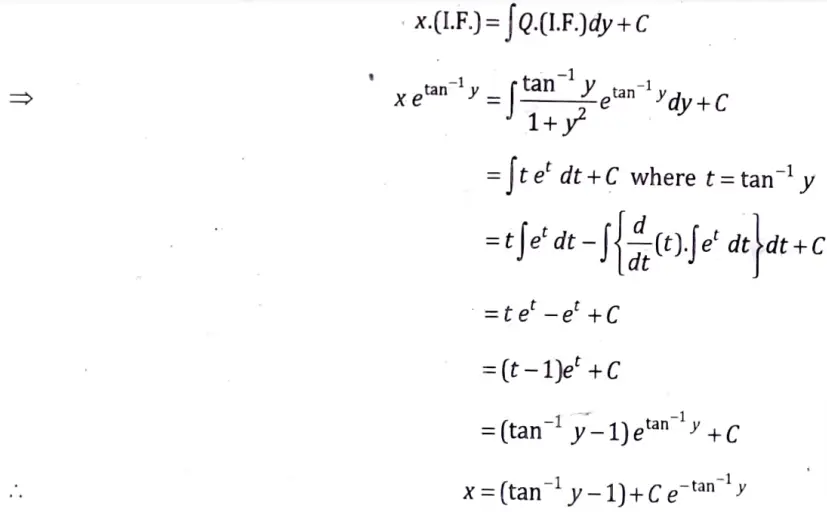
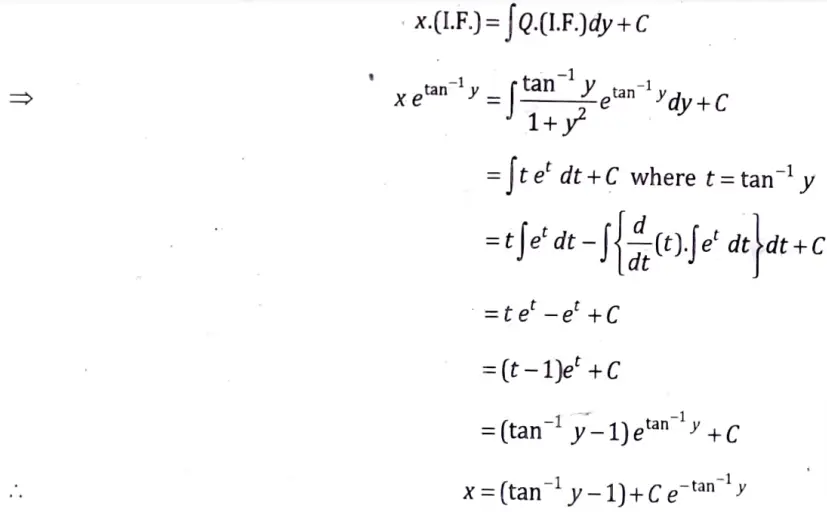
Which is the required solution. 

Q13. Solve

(D² + 1)y = sin x sin 2x

Sol. Here, the given equation is 

(D² + 1)y = sin x. sin2x

To find the C.F. of eq. (1), the auxiliary equation is 

(m² + 1) = 0 ⇒ m ± i

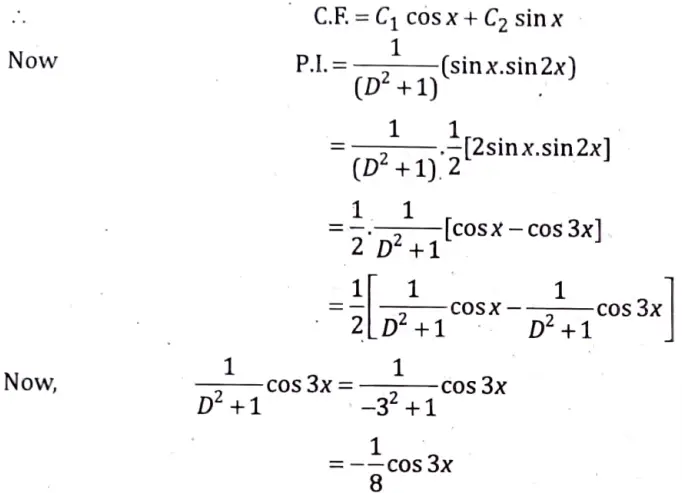
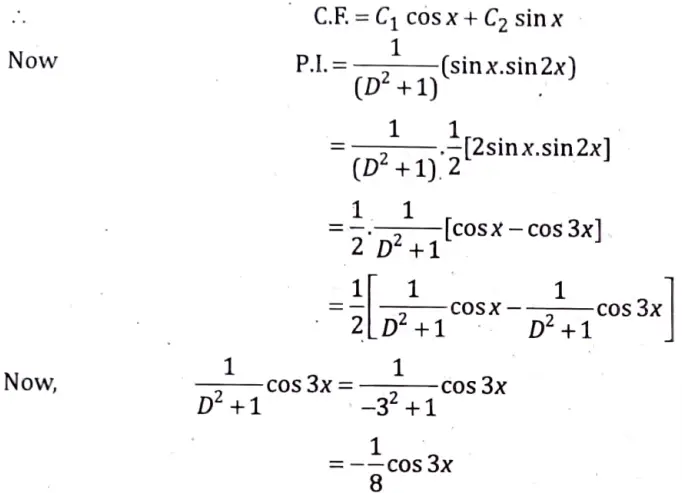
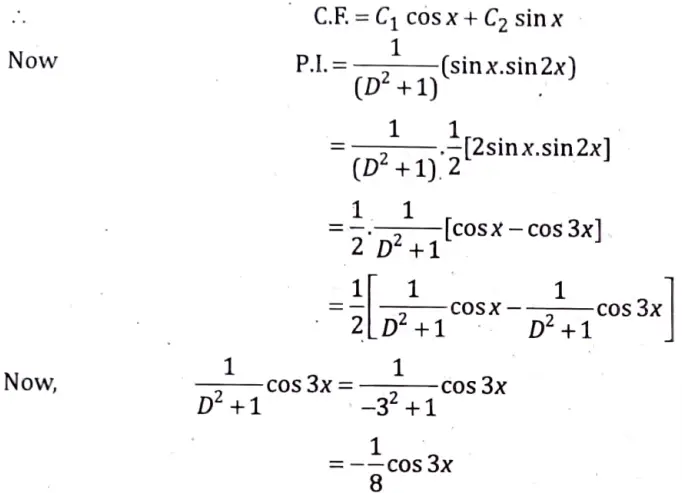
Hence, the complete solution of eq. (1) is given by

y = C.F.+ P.I.